Datenverarbeitungsgrundlagen & Statistik

Daten charakterisieren, aufbereiten und auswerten (Version: 11. Dezember 2021)

INHALTSVERZEICHNIS

1. Grundbegriffe
1.1 Begriffserklärung «Daten»
1.2 Der Zugriff auf «Daten»
1.3 Strukturierte versus unstrukturierte Daten
1.4 Diskrete, stetige und häufbare Merkmale
1.5 Skalentypen
1.6 Datentypen und Wertebereiche
1.7 Tabellenterminologie & Adressierung
1.8 JSON & XML

2. Daten grafisch darstellen
2.1 Einführung
2.2 Diagrammtypen
2.3 Diagrammbeschriftung
2.4 Manipulation von und mit Diagrammen
3. Statistik
3.1 Einleitung
3.2 Begriffe der Statistik
3.3 Wahrer Wert μ
3.4 Extremwerte Min, Max
3.5 Datenzahl
3.6 Häufigkeit/Histogramm
3.7 Lagekennzahlen Modus, Median, Mittelwert
3.8 Die Normal- oder Gauss-Verteilung
3.9 Streuungskennzahlen Spannweite, Varianz, Standardabweichung
3.10 Excel und Logik


1. Grundbegriffe

1.1 Begriffserklärung «Daten»

  • Daten: Sind Nachrichten, die maschinell verarbeitet und gespeichert werden können.
  • Nachricht: Wird unterschieden nach syntaktischem, semantischem und pragmatischem Aspekt. Übermittelte Daten sind Nachrichten.
  • Information: Ist in einer Nachricht enthalten und hat einen Neuigkeitswert.
  • Wissen: Bedeutet verknüpfte Information - Assoziationen.
  • Redundanz:
    • Redundanz (Informationstheorie), ohne Informationsverlust wegzulassende Informationen.
    • Redundanz (Kommunikationstheorie), mehrfache Nennung derselben Information.
      Redundante Informationen besitzen keinen Neuigkeitswert und sind in der Datenverarbeitung unerwünscht!
    • Redundanz (Technik), zusätzliche technische Ressourcen als Reserve wie z.B. ein zusätzliches Netzteil.
Daten für sich alleine stellen noch keine Informationen dar. Die Ziffernkombination «Fünf, Null» lässt den Wert 50 erkennen. Dieser Wert ist aber noch keine Information, Sie können damit noch nichts anfangen. Erst der Zusammenhang macht aus Daten Informationen

1.2 Der Zugriff auf «Daten»

Je besser eine Datenablage organisiert bzw. strukturiert ist, desto komfortabler gestalten sich die Zugriffe darauf. Die Erstellung einer starken Datenstruktur erfordert allerdings auch einen höheren Arbeitsaufwand. Die Datenverwaltung umfasst folgende Aktionen:
  • Daten erfassen: Neuer Datensatz hinzufügen.
  • Daten mutieren: Datensatz suchen und ändern/ergänzen.
  • Daten löschen: Datensatz vollständig entfernen
  • Daten auswerten: Datensatz suchen und analysieren, vergleichen etc.
  • Daten formatieren: Datenformat bestimmern (Datum, Zahl, Text etc.)

1.3 Strukturierte versus unstrukturierte Daten

Man unterscheiden zwischen unstrukturierten, wenig strukturierten und voll strukturierten Daten, wobei starke Strukturen für die Bewirtschaftung und Auswertung der Daten geeigneter sind.

  • Unstrukturiert: z.B. beliebiger Text. Ausser dem zur Verfügung stehenden Zeichensatz gibt es keine Einschränkungen bezüglich der Datenstruktur. Daher sind die Möglichkeiten einer Auswertung auch sehr beschränkt.
    • Initialaufwand: Klein. Texteditor starten und loslegen.
    • Erfassen: Wenig Aufwand da der Neuzugang nicht in eine Struktur eingefügt werden muss. Man legt einen neuen Eintrag einfach zuoberst auf den Stapel.
    • Mutieren, Löschen: Hoher Aufwand. Der Datensatz muss zuerst gefunden werden. Das bedeutet: Den ganzen Text Wort für Wort durchsuchen.
    • Auswerten: Hoher Aufwand. Datensatz und Vergleichsdatensatz muss zuerst gefunden werden. Siehe auch Mutieren.
  • Wenig strukturiert: Z.B. Karteikasten → als Blechbox mit Kundenkärtchen und alphabetischem Register (oder ein Telefonbuch, eine EXCEL-Tabelle)
    • Initialaufwand: Mittel. Es müssen eine Blechbox gezimmert, ein paar Kärtchen zugeschnitten und 26 Register-Einlagen von A-Z erstellt werden.
    • Erfassen: Mittlerer Aufwand da der Neuzugang nur in eine einfache Struktur eingefügt werden muss: Man ordnet die neue Karte alphabetisch gemäss z.B. "Familiennamen" ein. Dies hat aber schon ein höherer Aufwand zur Folge, als bei einer unstrukturierten Datensammlung.
    • Mutieren, Löschen: Mittlerer bis hoher Aufwand. Der Datensatz muss zuerst gefunden werden. Dies ist nun bedeutend einfacher als bei einer unstrukturierten Datensammlung. Allerdings nur dann, wenn genau nach dem sortierten Kriterium "Familiennamen" gesucht wird. Möchte man nämlich alle Kunden aus einem bestimmten Wohnort anschreiben, führt am durchblättern aller Kärtchen nichts vorbei.
    • Auswerten: Hoher Aufwand. Datensatz und Vergleichsdatensatz muss zuerst gefunden werden. Siehe auch Mutieren.
  • Strukturiert: Datenbank auf einem Computer.
    • Initialaufwand: Hoch. Das Datenmaterial muss eingehend analysiert und die geeignete Struktur definiert werden. Anschliessend: Installation der Datenbank-SW und Erstellen der Datenstruktur. (Tabellen/Grundgerüst)
    • Erfassen: Mittlerer Aufwand, da eine Struktur vorliegt.
    • Mutieren, Löschen und Auswerten: Kleinerer Aufwand. Datensatz kann im Idealfall nach beliebigem Kriterium gesucht werden.

1.4 Diskrete, stetige und häufbare Merkmale

  • Häufbares Merkmal: Ein Merkmal kann mehrere Ausprägungen annehmen.
    Bsp.: Personenbefragung → Hobby: Die Person kann unter Hobby mehrere Nennungen machen. (Lesen, Tanzen, Skifahren)
    Bsp.: Berufsausbildung → Die Person hat verschieden Ausbildungen absolviert. (Kochlehre, Hotelfachschule)
    Muss in tabellarische Struktur überführt werden.
  • Diskretes Merkmal: Merkmal hat abzählbar viele Ausprägungen bzw. die Anzahl der möglichen Ausprägungen ist endlich.
    Bsp.: Geschlecht, Haarfarbe, Anzahl der Teilnehmer/innen an einer Veranstaltung etc.
  • Stetiges Merkmal: Merkmal kann unendlich viele Ausprägungen annehmen.
    Bsp.: Wasserpegel, Gewicht, Strecke, Zeitintervall.

1.5 Skalentypen

  • Nominalskala: Meist diskret, häufbar. Daten können untereinander verglichen aber in keine natürliche Reihenfolge gebracht werden. Bsp.: Geschlecht, Kontonummer, Haarfarbe, Telefonnummer, Geschmacksrichtung.
  • Ordinalskala: Meist diskret, nicht häufbar. Können im Gegensatz zu nominalskalierten Daten in eine natürliche Reihenfolge gebracht werden. Die Abstände zwischen den einzelnen Werten sind nicht quantifizierbar. Berechenbar mit Vorbehalt.
    Bsp.: Präferenzrangfolgen, Zufriedenheit (z.B. auf einer Skala von 1 bis 5), Dienstrang.
  • Kardinalskala (Metrische Skala): Meist stetig, nicht häufbar. Verfügen über eine natürliche Reihenfolge und quantifizierbaren Abständen. Berechenbar.
    Bsp.: Zeitdauer, Wassertiefe, Streckenlänge.

1.6 Datentypen und Wertebereiche

Datentypen:

Der Datentyp sagt aus, wie die im Computer binär vorliegenden bzw. verarbeitbaren Daten zu interpretieren sind. Die allgemeinen Datentypen:

  • Integer: Ganzzahl, ursprünglich 16 Bit = 216 Kombinationen und somit -32'768 .. + 32'767, Operationen: + - * / < > = % (%=Modulo)
  • Boolean: Wahr oder Falsch bzw. 1 oder 0, Operationen: NOT AND OR = (und Kombinationen davon)
  • Character: Alphanumerisches Zeichen, Satzzeichen (ASCII), Operationen: < > = StrToInt
  • Floating-point numbers: Fliesskommazahl oder Dezimalzahl in der Form ±0.xxx E±yyy, Operationen: + - * / < > =
  • Alphanumeric string: Zeichenkette oder Array of char

Weitere spezielle und zusammengesetzte Datentypen:

  • Enumeration: Aufzählungstypen wo der Wertebereich selber definiert werden kann (z.B. Rot, Grün, Gelb, Blau, Schwarz, Weiss)
  • Record: Struktur, die ihrerseits verschiedene Datentypen enthält

Einige der zusätzlichen Zahlenformate in z.B. Excel:

  • Currency: Währung (z.B. CHF 23.40)
  • Date: Datum (z.B. Mittwoch, 14 März 2012)
  • Time: Zeit (z.B. 13:30 h)
  • Prozent: (z.B. 80.3%)

Wertebereiche:

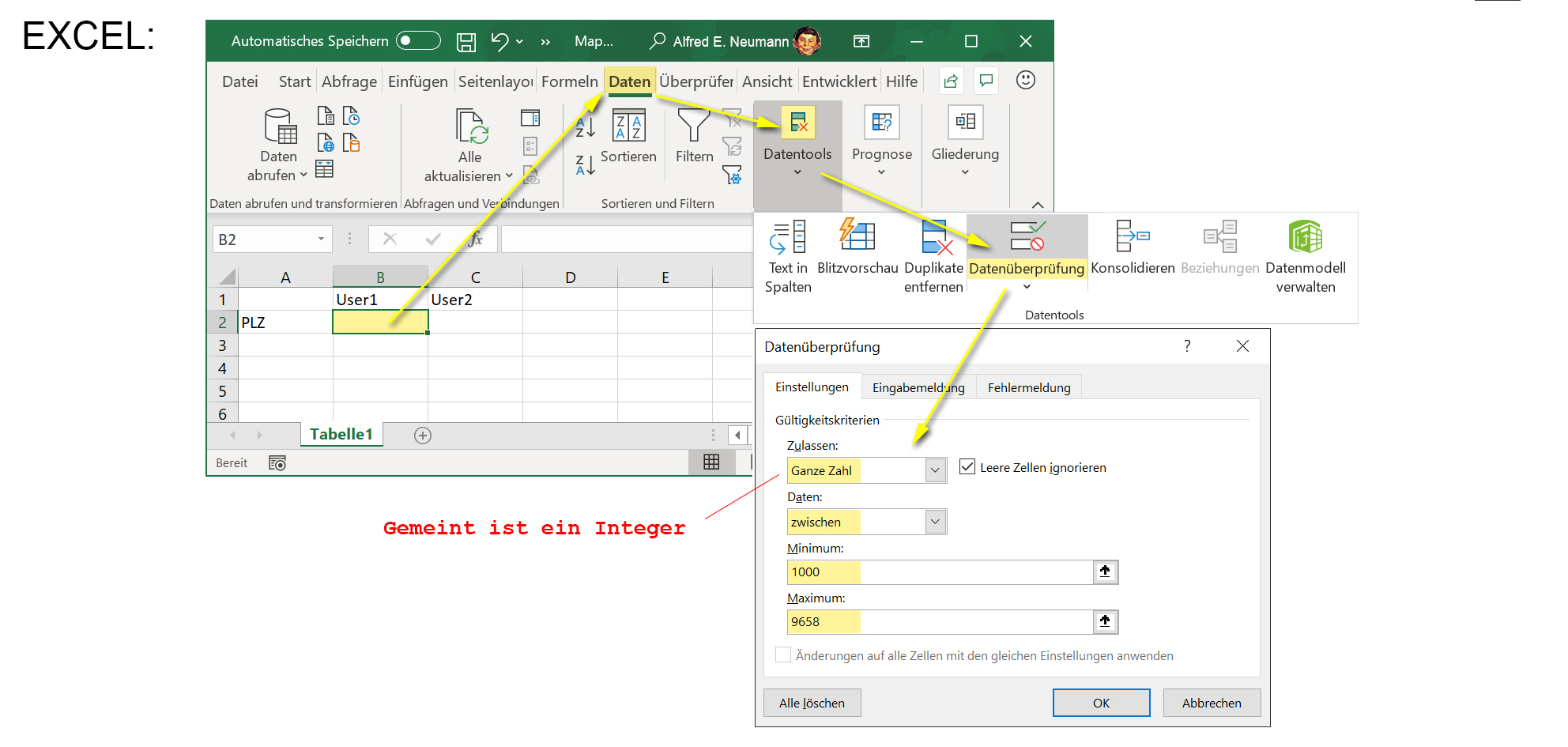
Abgesehen davon, dass Datentypen wie der Integer keine unendlichen Wertebereiche haben, kann auch die Aufgabe eine Einschränkung der einzugebenden Daten erfordern. Zum Beispiel beginnen die Schweizer Postleitzahlen bei 1000 (Lausanne, VD) und enden bei 9658 (Wildhaus, SG). Somit kann man schon bei der Eingabe durch die Einschränkung «1000≤PLZ≤9658» verhindern, dass inexistente Postleitzahlen erfasst werden. (Plausibilität)

Datentypen in EXCEL

So werden im Tabellenkalkulationsprogramm EXCEL Datentypen definiert und auch gleich im Wertebereich eingeschränkt:

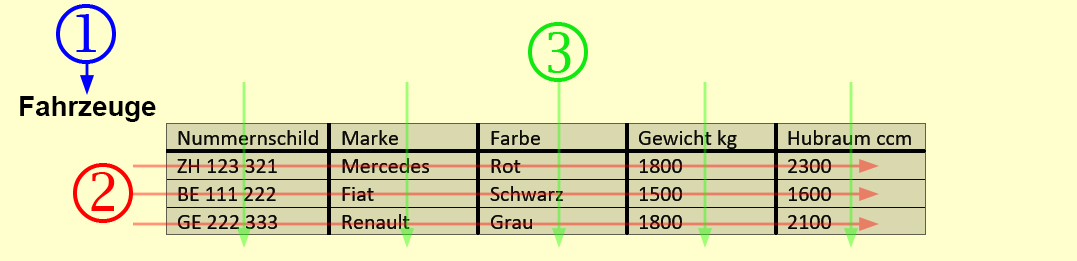
1.7 Tabellenterminologie & Adressierung

Diese Begriffe mus man kennen:

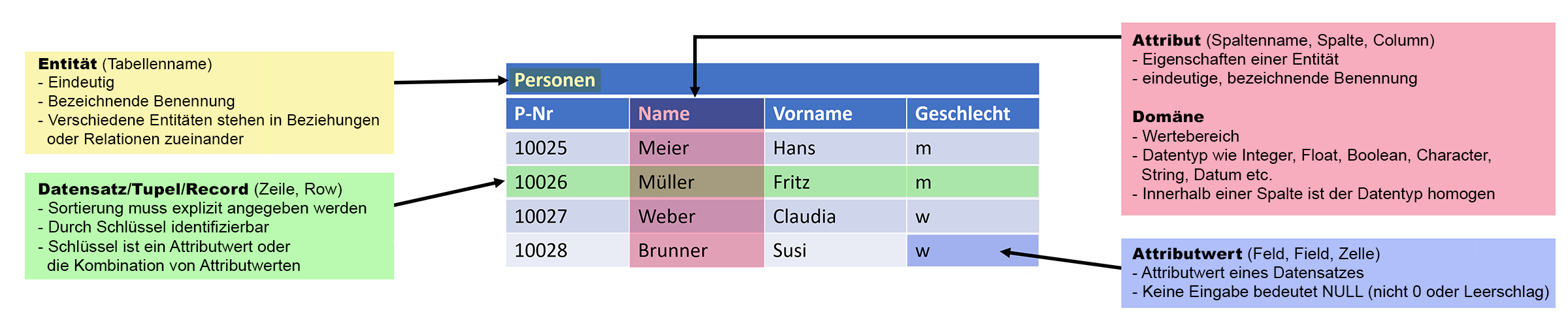
Und so werden Daten in einer Tabelle gefunden (Dreistufige Adressierung):


1.8 JSON & XML

  • JSON: JSON (JavaScript Object Notation) ist ein kompaktes Datenformat in einer einfach lesbaren Textform für den Datenaustausch zwischen Anwendungen. JSON ist von der Programmiersprache unabhängig. Parser und Generatoren existieren in allen verbreiteten Sprachen. Weiterführende Info (Einführung, Tutorials, Tools) siehe Link-Seite → INFORMATIK-Links.
  • XML: XML (Extensible Markup Language) ist wie JSON eine Auszeichnungssprache zur Darstellung hierarchisch strukturierter Daten im Format einer Textdatei. XML wird auch für den plattform- und implementationsunabhängigen Austausch von Daten zwischen Computersystemen eingesetzt, insbesondere über das Internet.
Die Syntax von JSON ist sehr viel einfacher gestaltet als XML und erscheint daher oft lesbarer und insbesondere leichter schreibbar. In der Regel produziert JSON auch geringeren Overhead im Vergleich zu XML.

JSON-Beispiel

Im folgenden zwei Beispiele, wie JSON eingesetzt werden kann:

  • In Beispiel 1 werden die Datensätze nicht direkt in HTML angezeigt. Dazu muss man im Webbrowser die Konsole mit der Funktionstaste F12 öffnen. Danach in der neu angezeigten Menueleiste die «Konsole» wählen und Array(4) öffnen.
  • In Beispiel 2 werden die Datensätze direkt in HTML ausgegeben.
  • Beispiel 1 & 2 im Webbrowser anzeigen.
Der HTML-Code inkl. JSON-Teil:


Praxisaufgabe ∇ AUFGABEN
∇ LÖSUNGEN

2. Daten grafisch darstellen

2.1 Einführung

Warum Daten visualisieren?

Durch die Visualisierung wird beim Betrachter eines Diagramms ein zusätzlicher Kanal angesprochen. Man nutzt also die Erkenntnis, dass sich Denkoperationen auch in Bildern vollziehen können. Da die bildliche Wahrnehmung beim Menschen stark ausgeprägt ist, erhält man durch die Visualisierung von Daten folgende Vorteile:

  • Es bringt die Möglichkeit, das Wesentliche in einer kompakten Form zu zeigen
  • Sie erhöhen die Verständlichkeit - Man sieht das Wesentliche auf einen Blick
  • Durch das Aufzeigen von Grössenverhältnissen wirken die Zusammenhänge oft eindrücklicher
  • Dank unserem guten visuellen Gedächtnis erinnern wir uns später besser daran
  • In einem Bericht bewirken sorgfältig eingesetzte Diagramme oft einen besseren Gesamteindruck
  • Diagramme werden oft zur Manipulation der Betrachter herbeigezogen

2.2 Diagrammtypen

Daten können auf verschiedene Arten dargestellt werden:

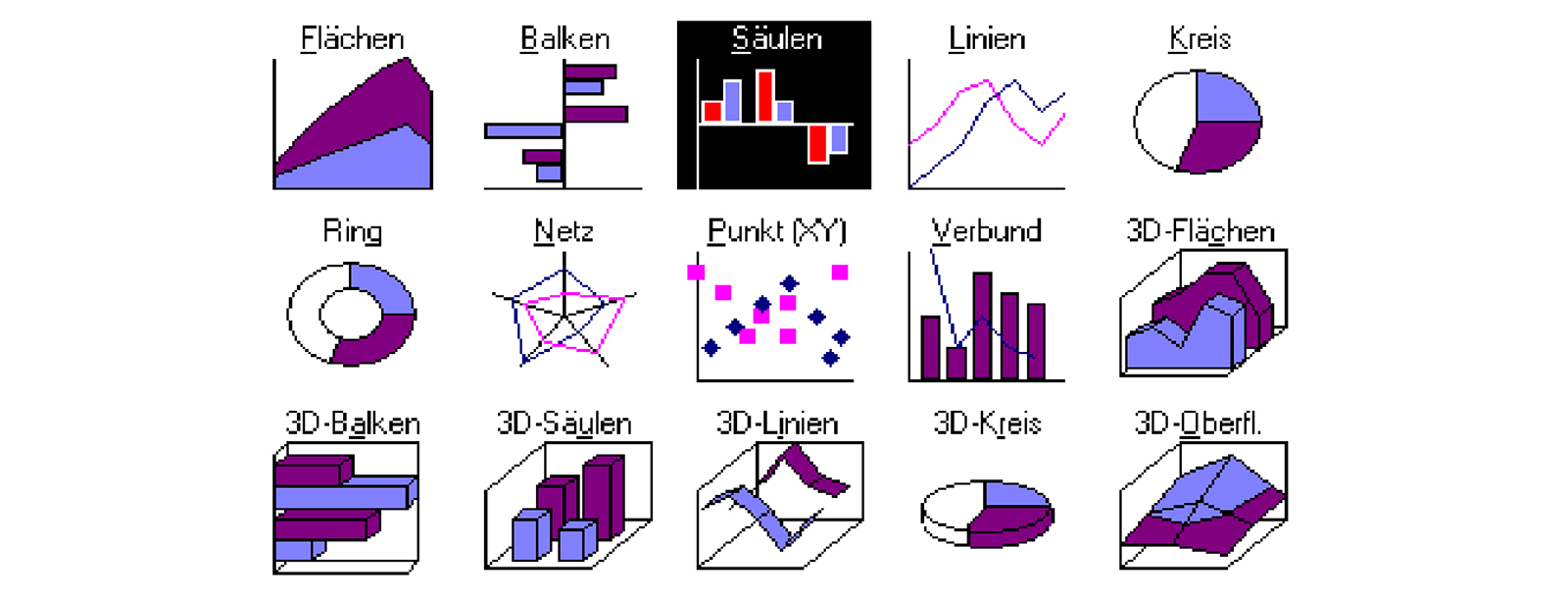
  • Liniendiagramme: Sind wohl die bekanntesten Vertreter von Diagrammen. Sie sind besonders stark verbreitet in Mathematik und Physik aber auch bei Börsenkursen. Man versucht anhand der Kurvenverläufe Messungen und komplizierte Berechnungen besser zu verstehen oder wagt damit Prognosen. Typischerweise steigen die Werte in beide Achsenrichtungen kontinuierlich an. Jedem Punkt in der Diagrammebene kann man somit zwei Werte zuordnen. Man kann der Kurve entlangfahren und zu jeder beliebigen Position das aktuelle Wertepaar ablesen.
  • Balken– und Säulendiagramme: Beises ist im Prinzip dasselbe. Es werden einzig die beiden Achsen vertauscht. Balkendiagramme sind dann geeignet, wenn die Legenden der Rubrikenachse lang sind und (oder) man viele Rubriken hat. Jeder Gruppe wird ein Wert zugewiesen.
  • Kreisdiagramme: Diese (in dreidimensionaler Darstellung nennt man sie Tortendiagramme) sind dann geeignet, wenn man die verschiedenen Anteile von etwas Ganzem anzeigen möchte. Typisch z.B. zur Darstellung von Umfrageergebnissen.

2.3 Diagrammbeschriftung

Bezeichnungen und Begriffe in Diagrammen:

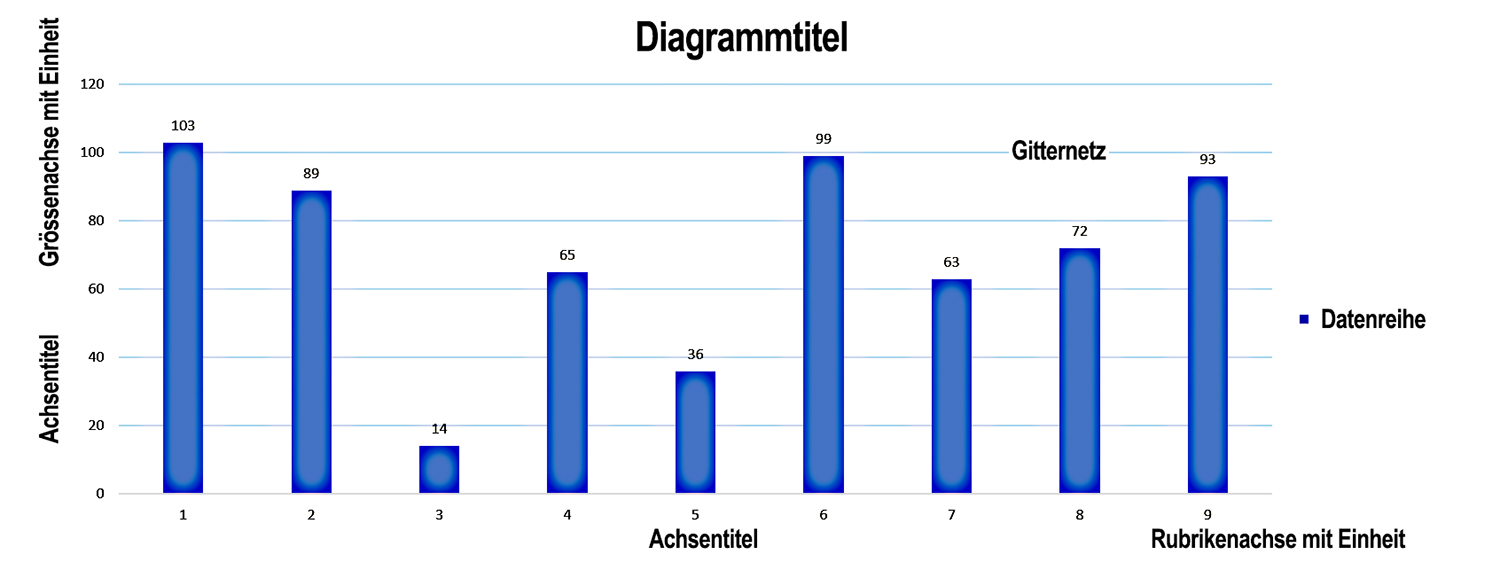
Ein paar EXCEL-Grafikbeispiele:

Diese EXCEL-Datei mit den Grafikbeispielen hier herunterladen.


Praxisaufgabe ∇ AUFGABEN
∇ LÖSUNGEN


2.4 Manipulation von und mit Diagrammen

Hinter bewusster Manipulation von Diagrammen steht die Absicht, gewissen Aspekten der Datenlage ein besonderes Gewicht zu geben. Mögliche Schlüsse sollen sich auffällig präsentieren oder man möchte gewisse Facts möglichst vertuschen. Der Betrachter erkennt oft nur beim aufmerksamen Studieren die wahren Absichten hinter solchen Verfälschungen. Hier einige beliebte Tricks:

  • Weglassen von einzelnen Diagrammelementen. (z.B. fehlt die Achsenbeschriftung)
  • Ungleichmässige Abstände auf der Grössenachse.
  • Verwenden von logarithmischen Skalen.
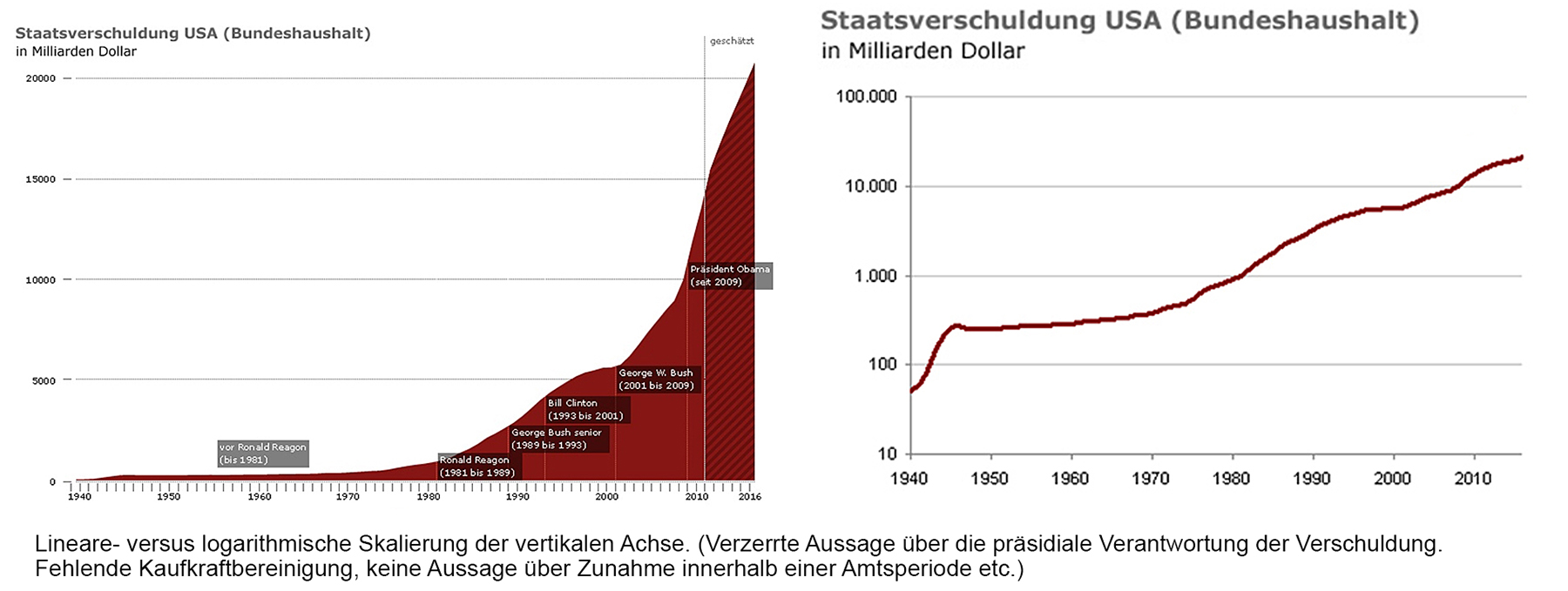
  • Fokus (dargestellten Bereich) variieren - Damit kann man aus feinen Unterschieden grosse Sprünge machen und umgekehrt.
  • Bei Säulendiagrammen kann man für einen doppelt so grossen Wert, nebst der doppelten Höhe der Säule auch deren Breite noch vergrössern. (Ist die Breite z.B. 1.5 mal so gross, so wächst die Fläche bereits auf das 4.5 fache.)
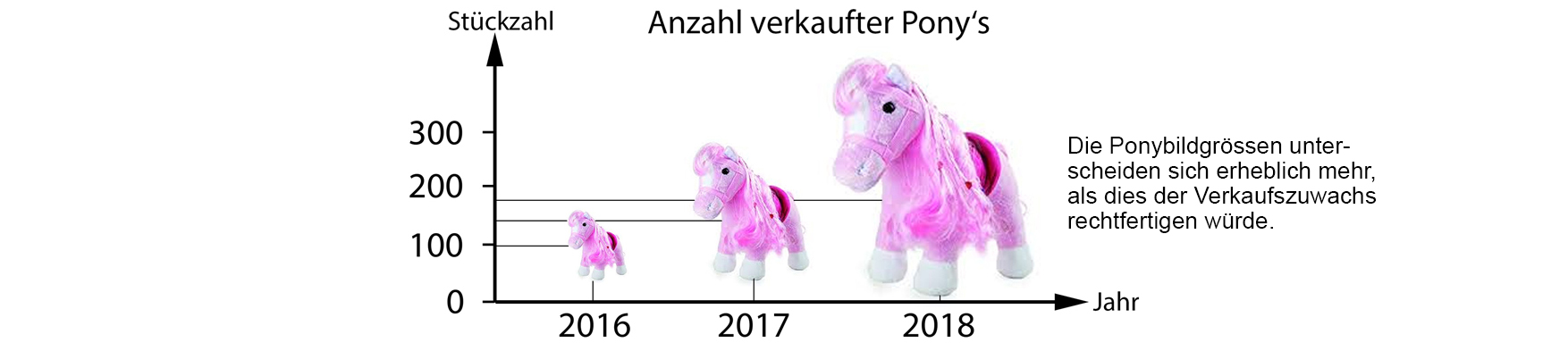
  • Visuell gewisse Teilaspekte besonders hervorheben - Oft lässt sich mit der Farbwahl der einzelnen Elemente bereits etwas erreichen.
  • Verfälschen des ersten Eindrucks über die Grössenverhältnisse durch 3D-Ansichten.
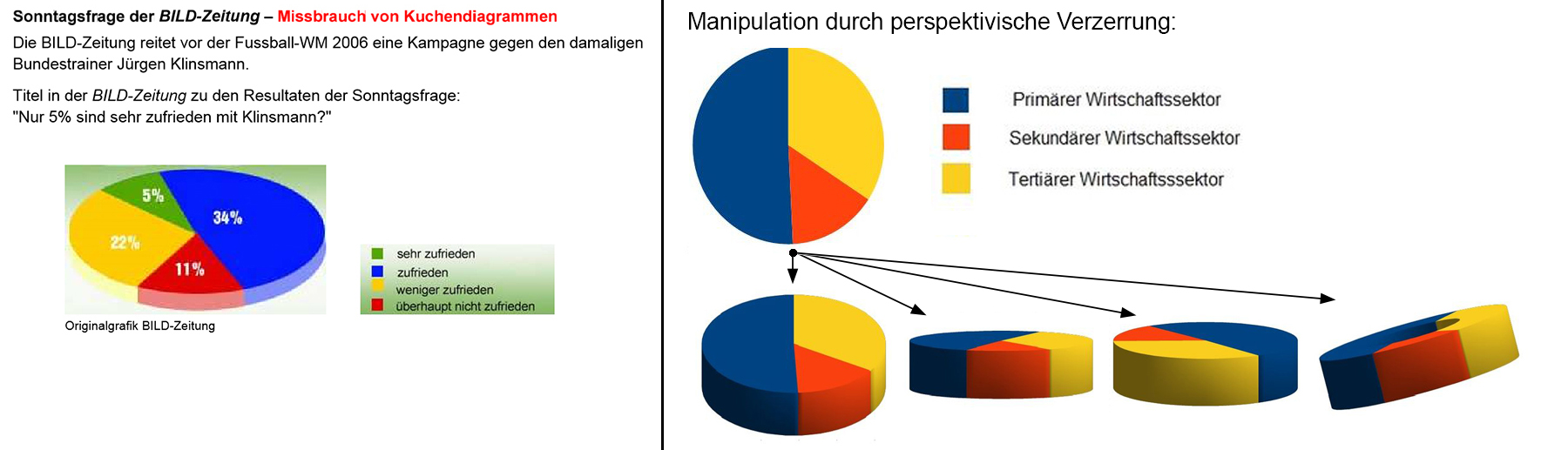
  • Weitere Beispiele:
Praxisaufgabe ∇ AUFGABE
∇ LÖSUNG

3. Statistik

3.1 Einleitung

Ferien auf Pandora

Ihre Ferien auf Pandora gehen zu Ende. Zuhause angekommen erfahren sie, dass man von Pandora neben Erinnerungen an traumhaft neonfarbene Flora und Fauna auch ein Souvenir in Form einer seltenen Krankheit mitbringen kann, in deren Verlauf sich die menschliche Haut blau verfärbt. Da die Heilungschancen bei einer Früherkennung gross sind und sie in Zukunft nicht wie ein Schlumpf herumlaufen möchten, entschliessen sie sich, bei ihrem Hausarzt einen Test durchführen zu lassen. Dieser fällt leider positiv aus. Dies bedeutet, dass Hinweise auf die Krankheit gefunden worden sind. Ihr Arzt gibt ihnen zusätzlich folgende Informationen:

  1. Zuverlässigkeit des Tests: 99 von 100 Infizierten werden erkannt. Ein Infizierter wird übersehen.
    (In 99 Prozent der Untersuchungen von Erkrankten liefert der Test ein positives/richtiges, in 1 Prozent der Fälle ein negatives/falsches Ergebnis.).
  2. Von 100 Nichtinfizierten werden 98 als tatsächlich gesund erkannt. Zwei geraten fälschlich in Verdacht, krank zu sein (...und zu denen möchten Sie gehören).
    (Der Test liefert somit in 98 Prozent der Untersuchungen Gesunder ein negatives/richtiges und in 2 Prozent ein positives/falsches Ergebnis.)
  3. Die Krankheit tritt nur etwa bei jedem tausendsten Tourist/in auf. Symptome sind aber erst nach einer gewissen Zeit erkennbar.
    Bisher wurden 200'000 Reiserückkehrer/innen getestet.
  4. Da ihr Testergebnis positiv war, wird zur weiteren Abklärung ein umfassender Untersuch unter Vollnarkose erforderlich.
Der Test identifiziert also mit 99-prozentiger Sicherheit die Erkrankten und mit 98-prozentiger Sicherheit die Gesunden. Er ist also sehr zuverlässig und er ist bei ihnen positiv ausgefallen. Besteht nun Grund, sich ernsthaft Sorgen zu machen?

Und hier die Auflösung zu «Ferien auf Pandora»:

Die Wahrscheinlichkeit der Erkrankung wird darum oft zu hoch eingeschätzt, weil man die Genauigkeit der Tests anschaut, ohne die Häufigkeit der Krankheit zu berücksichtigen. Der statistische Fachbegriff dafür lautet Prävalenz. Im unserem Fall ist unter Punkt 3 beschrieben, dass die Krankheit nur bei jedem tausendsten Reisenden auftritt: Somit ist die Prävalenz 1 Erkrankter auf 1000 Personen. (Korrekt spricht man von der Prävalenzratio: das ist die Anzahl Erkrankter durch die Anzahl untersuchter Personen.) In unserem Beispiel sind von 200'000 Personen deren 200 wirklich erkrankt. 99% dieser Erkrankten werden durch den Test auch erkannt: In diesem Fall 198 Personen. 2% geraten fälschlicherweise in Verdacht, erkrankt zu sein, sind es aber nicht: 2% von 199'800 gesunden Personen (3996 Personen) erhalten zusätzlich eine Positiv-Meldung. Von den 4196 Meldungen (100%) sind aber nur 200 wirklich erkrankt: Somit 4.77%.



Es ist unser Ziel, Ergebnisse von statistischen Erhebungen und grosse Datenmengen so zusammenzufassen, dass sie einfach zu interpretieren sind und das Wesentliche in möglichst knapper Form aussagen. Neben der graphischen Darstellung gibt es eine Reihe von statistischen Masszahlen mit denen wir dieses Ziel erreichen können. Das arithmetische Mittel (bzw. Durchschnitt) ist sicher allen bekannt. Auch wenn er eine rechnerisch klar definierte Grösse ist, ist seine Aussagekraft nicht immer eindeutig. Einige dieser Masszahlen werden im Folgenden Thema sein.

3.2 Begriffe der Statistik

  • Messwert: Gemessener, beobachteter oder abgelesener Wert. Es handelt sich um die Quantität, welche erhoben wird. (z.B. Grösse in m)
  • Ergebnis: Ergebnis einer Analyse nach der Durchführung der Messung und aller nachfolgender Auswertungsschritte. (z.B. Durchschnittsgrösse)
  • Zufallsvariable: Variable, mit der wir das Ergebnis eines noch nicht durchgeführten Zufallsexperiments beschreiben Eine Zufallsvariable lässt sich durch eine Wahrscheinlichkeitsfunktion berechnen. Der Wert der Zufallsvariable soll möglichst nahe am wahren Wert liegen.
  • Grundgesamtheit: Jede Zufallsvariable gehört zu einer unendlich grossen Menge möglicher Zufallsvariablen. Diese wird als Grundgesamtheit bezeichnet.
  • Stichprobe: Eine begrenzte Menge aus der Grundgesamtheit wird Stichprobe genannt.

3.3 Wahrer Wert μ

Der wahre Wert einer Menge ist theoretisch und kann normalerweise nie exakt bekannt sein. Es ist der Wert, den man in einer perfekten Messung erhalten würde. Wahre Werte sind naturgemäss unbestimmt.
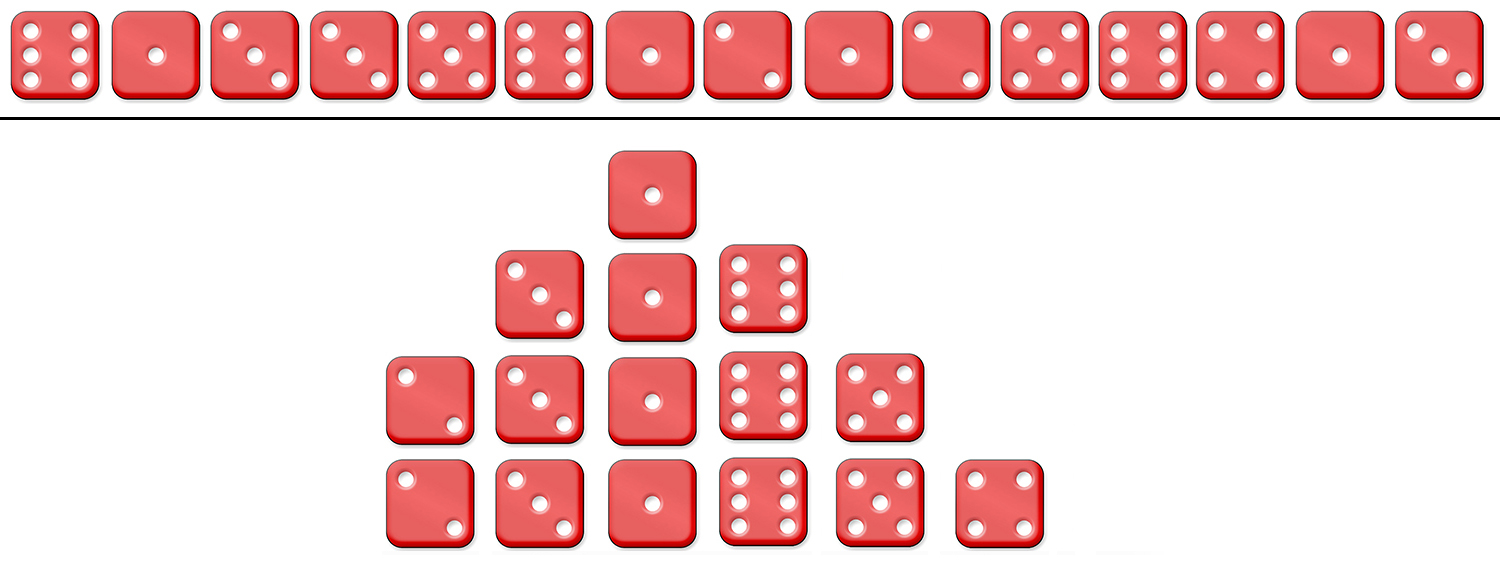
Im folgenden Würfelbeispiel entspricht der wahre Wert 3.5 → (1+2+3+4+5+6)/6. Dies bedeutet, dass man bei einem idealen Würfel im Mittel 3.5 erhalten sollte, wenn man unendlich oft würfelt. Erhält man jedoch bei unendlich vielen Würfen nicht 3.5 als Mittelwert, dann ist die Differenz der sogenannte Bias «b» → systematischer Fehler. Durchschnitt: 6+1+3+3+5+6+1+2+1+2+5+6+4+1+3=49 49/15=3.27

3.4 Extremwerte Min, Max

  • Maximum: Grösster vorkommender Wert einer Stichprobe.
    = MAX(Bereich)
  • «k»-grösste Zahl z.B. drittgrösste Zahl (k=3)
    =KGRÖSSTE(Bereich,k)
  • Minimum: Kleinster vorkommender Wert einer Stichprobe
    = MIN(Bereich)

Weitere Extremwerte sind als Ausreisser erkannte Proben. Diese sind am besten in einem Säulendiagramm erkennbar.

3.5 Datenzahl

Die Anzahl an Zufallsvariablen wird als Datenzahl «n» bezeichnet.

  • = ANZAHL(Bereich) → Zählt Zahlen in Zellen!
  • = ANZAHL2(Bereich) → Zählt Anzahl nicht leere Zellen!
Im folgenden Würfelbeispiel 15, da man 15 Mal gewürfelt hat oder 15 Würfel mit einer angezeigten Würfelzahl vorliegen hat:

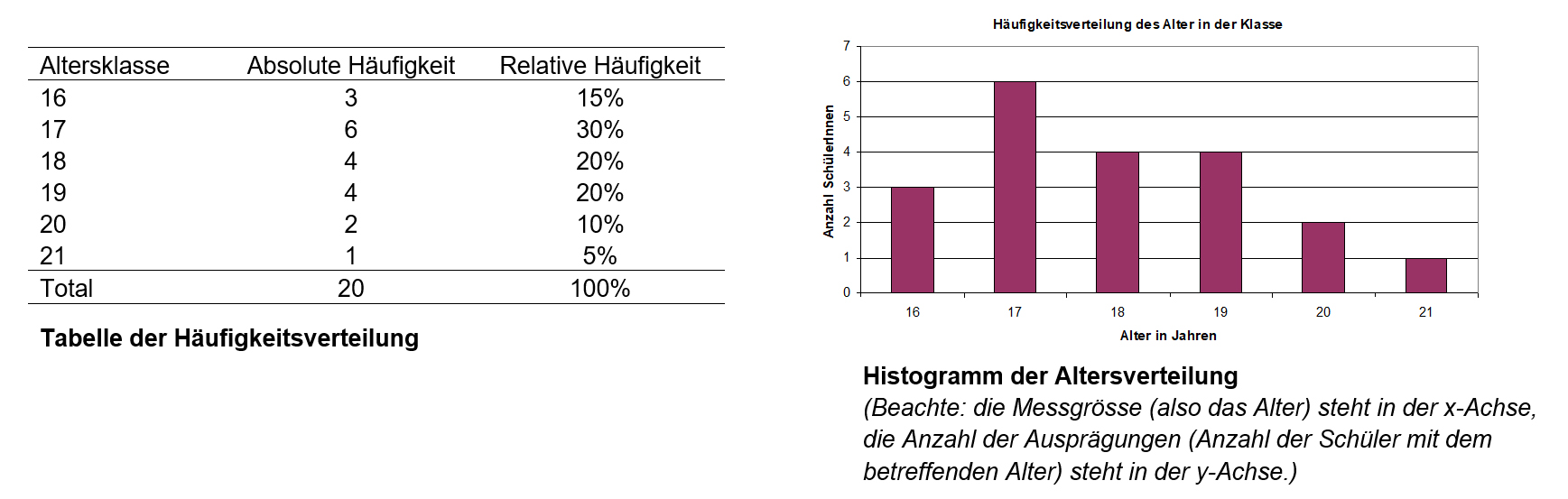
3.6 Häufigkeit/Histogramm

Die Häufigkeit «f» gibt an, wie oft ein Wert in der Stichprobevorkommt. Die Häufigkeit kann am besten in einem Säulendiagramm dargestellt werden. Das Häufigkeits-Säulendiagramm wird auch Histogramm genannt.

  • EXCEL Variante 1: (Manuell)
    Neue Tabelle mit folgendem Eintrag zu jeder Häufigkeitssäule:
    = ZÄHLENWENN(Bereich,"Klassenwert")
    (siehe auch =HÄUFIGKEIT())
  • EXCEL Variante 2: (Automatisch):
    ⇒ Daten ⇒ Datenanalyse ⇒ Histogramm: erzeugt neue Tabelle mit Häufigkeitswerten und Klassen (eigene Tabelle)
    (Hinweis: Falls Datenanalyse im Excel-Menu fehlt: Datei ⇒ Optionen ⇒ Add-Ins ⇒ Analyse Funktion anklicken ⇒ Gehe zu ⇒ Analyse Funktionen ( + VBA) anklicken ⇒ OK)
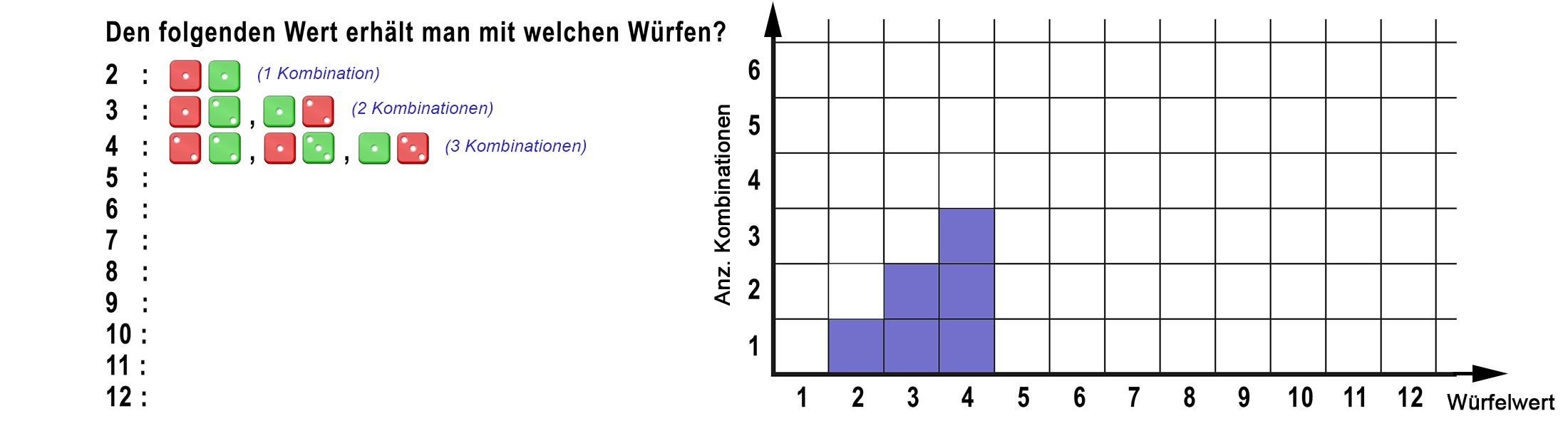
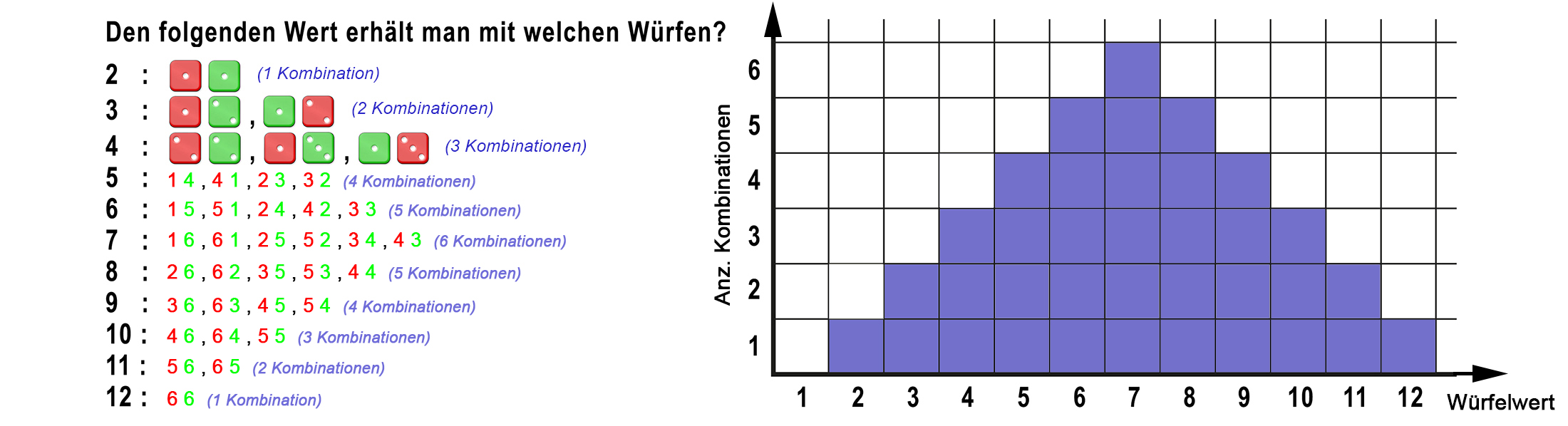
(Bei grösserer Spannweite können auch Wertebereiche (Klassen) anstelle von einzelnen Werten gewählt werden. (z.B. 1-2, 3-4, 5-6))

Das Histogramm des folgenden Würfelbeispiels:

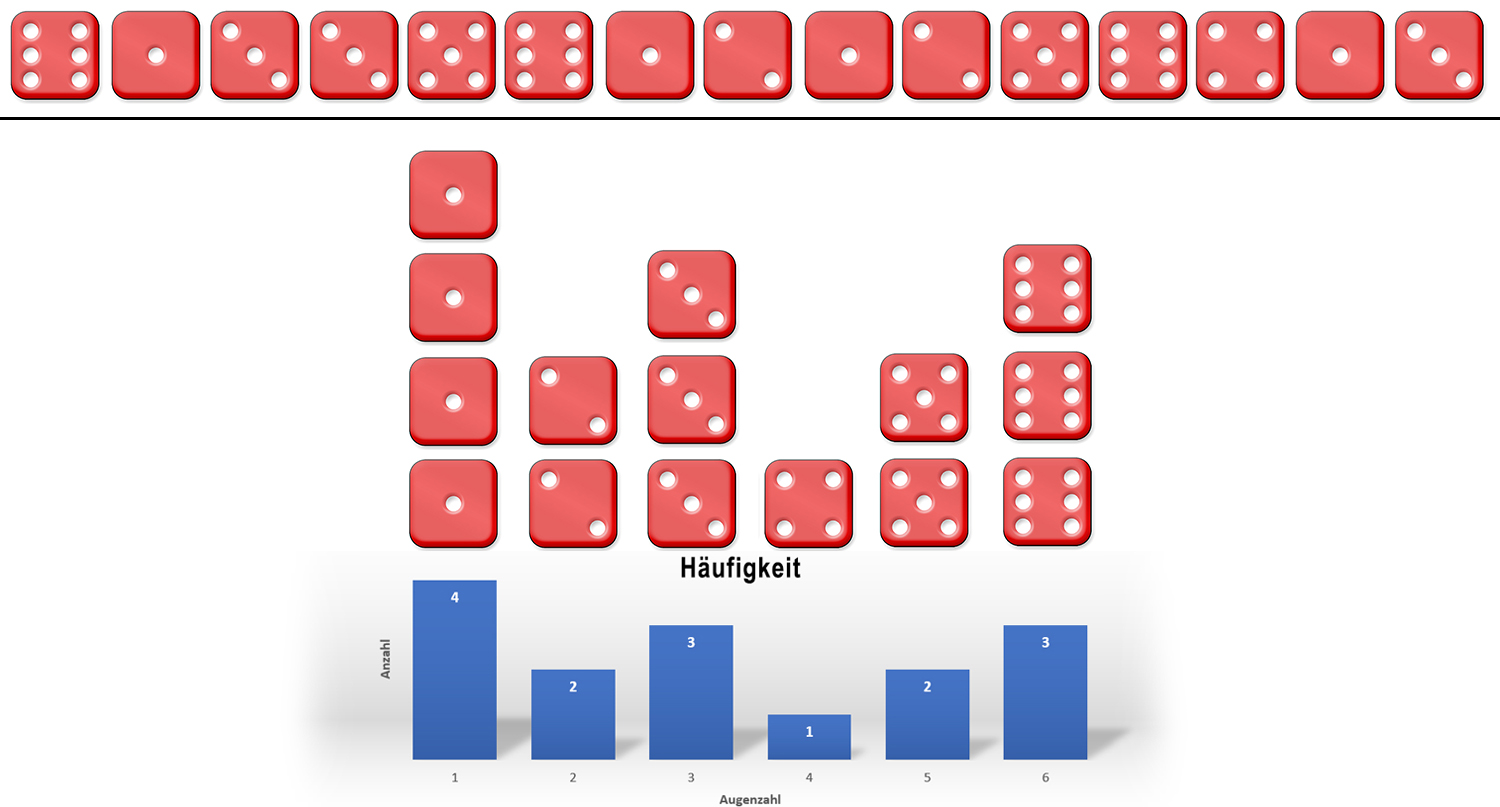
Extras ∇ WEITERE HISTOGRAMM-BEISPIELE

Praxisaufgabe ∇ AUFGABEN
∇ LÖSUNGEN


3.7 Lagekennzahlen Modus, Median, Mittelwert

Häufig genügt zur Charakterisierung der statistischen Masse die Darstellung der Häufigkeitsverteilung nicht. Man zieht oft zusätzliche Lagemasse heran, die eine Vorstellung über die mittleren Werte einer Verteilung geben sollen. Diese Mittelwerte werden nach zwei verschiedenen Kriterien charakterisiert: Lagetypische Mittelwerte, die von dem in der Mitte der Verteilung liegenden Wert bestimmt werden, wie Modus (häufigster Wert) und Median (zentraler Wert) und rechentypische Mittelwerte, wo jeder einzelne Wert der Verteilung berücksichtigt wird, wie z.B. beim arithmetischen Mittelwert.

  • Der Modus/Modalwert (Lagetypischer Mittelwert):
    Als Modus wird der mit der grössten Häufigkeit auftretende Wert bezeichnet. Er wird auch als dichtester Wert bezeichnet.
    = MODALWERT(Bereich)
    Im folgenden Würfelbeispiel erscheint der Modus als grösste Säule → Die Würfelzahl = 1.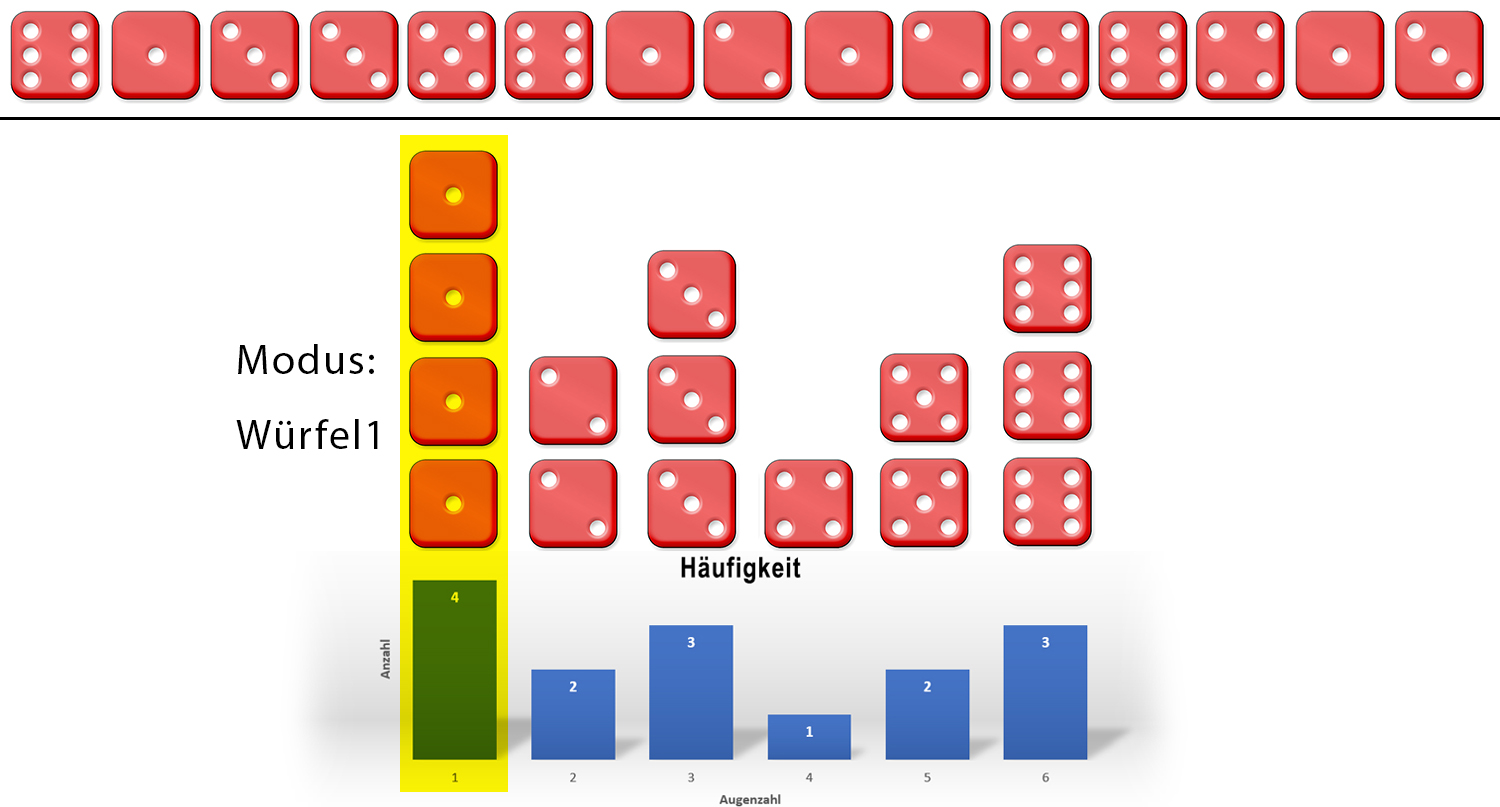
  • Der Median (Lagetypischer Mittelwert):
    In einer sortierten Liste der Stichproben ist der Median (Zentralwert) der mittlere Wert der sortierten Liste. Bei einer geraden Anzahl der Stichproben ist der Modus der Mittelwert der mittleren zwei Werte.
    = MEDIAN(Bereich)
    Im folgenden Würfelbeispiel ist der Median der mittlere Würfel 3
  • Der Mittelwert (Rechentypischer Mittelwert):
    Der Mittelwert wird auch weitläufig als Durchschnitt oder arithmetisches Mittel bezeichnet. Er wird berechnet, indem man alle Daten aufsummiert und durch die Datenanzahl teilt. Bei n Daten xi ergibt sich die Formel:
    = MITTELWERT(Bereich)
    Der Mittelwert im folgenden Würfelbeispiel ergibt 3.27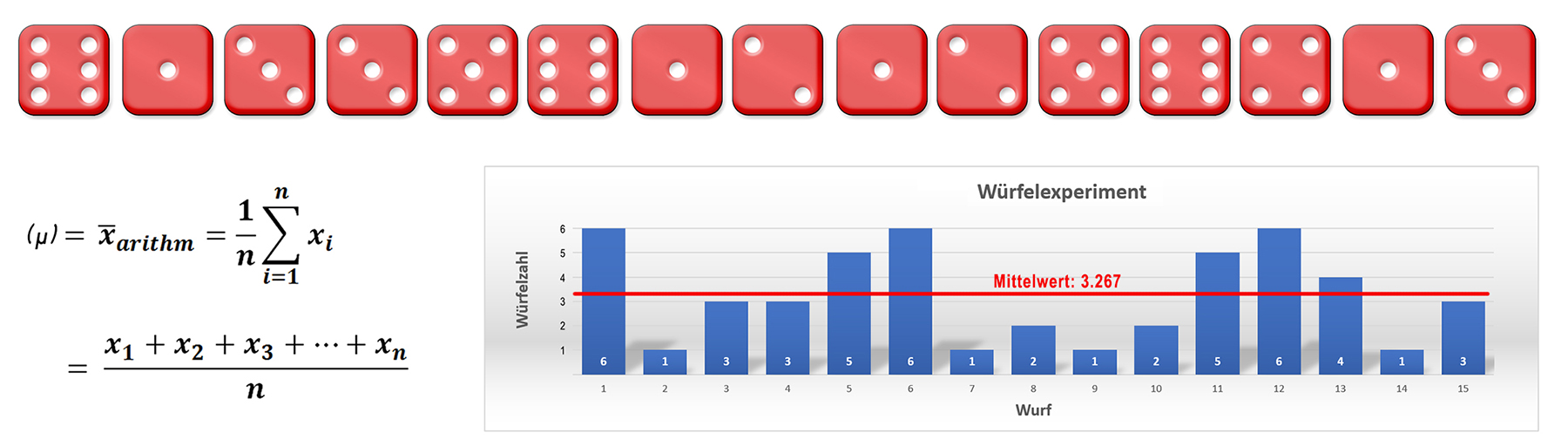

Praxisaufgabe ∇ AUFGABEN
∇ LÖSUNGEN


3.8 Die Normal- oder Gauss-Verteilung

Die Normal- oder Gauss-Verteilung wird auch Glockenkurve genannt. Die Abweichungen der Messwerte vieler natur-, wirtschafts- und ingenieurswissenschaftlicher Vorgänge vom Mittelwert lassen sich durch die Normalverteilung (bei biologischen Prozessen oft logarithmische Normalverteilung) entweder exakt oder wenigstens in sehr guter Näherung beschreiben. In der Versicherungsmathematik ist die Normalverteilung geeignet zur Modellierung von Schadensdaten im Bereich mittlerer Schadenshöhen. In der Messtechnik wird häufig eine Normalverteilung angesetzt, die die Streuung der Messfehler beschreibt. Hierbei ist von Bedeutung, wie viele Messpunkte innerhalb einer gewissen Streubreite liegen.
Die Normalverteilung ist durch die Wahrscheinlichkeitsdichte gegeben, wobei μ dem wahren Erwartungswert entspricht und σ die Standardabweichung darstellt, die die Breite der Normalverteilung beschreibt. 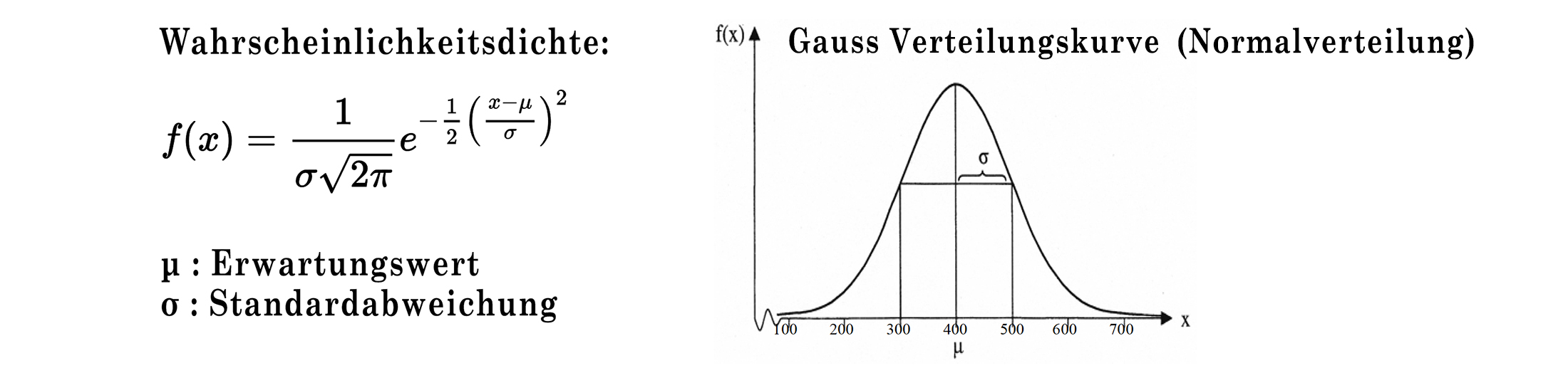Die Normalverteilung im folgenden Würfelbeispiel:

Praxisaufgabe ∇ AUFGABEN
∇ LÖSUNGEN


3.9 Streuungskennzahlen Spannweite, Varianz, Standardabweichung

Zur statistischen Charakterisierung einer untersuchten Zahlenreihe kann die Angabe einer Streuungskennzahl ebenso wichtig sein. Diese soll angeben, um wie viel die einzelnen Werte einer untersuchten Reihe voneinander oder von einem errechneten Mittelwert abweichen. Die Streuungskennzahlen werden u.a. benötigt, weil sie als Ergänzung zum Mittelwert die zentrale Tendenz einer Reihe erkennen lassen. Zu den statistischen Kennzahlen, die über eine solche Streuung Auskunft geben, zählen die Spannweite, die Varianz und die aus der Grundgesamtheit oder Stichproben berechnete Standardabweichung.

  • Die Spannweite:
    Die Spannweite (Range) wird als Differenz zwischen grösstem und kleinstem Wert einer Stichprobe definiert.
    R=xmax-xmin
    = MAX (Bereich) - MIN (Bereich)
    Im folgenden Würfelbeispiel ergäbe die Spannweite R=6-1; R=5
  • Die Varianz:
    Die bisher besprochenen Charakterisierungsmöglichkeiten einer Streuung reichen zwar für viele Problemstellungen aus. Für andere Problemstellungen ist jedoch ein Mass erforderlich, das alle Werte berücksichtigt. Die Werte der Grundgesamtheit 1 2 4 5 und 2.7 3.0 3.1 3.2 haben beide den Mittelwert 3, unterscheiden sich aber trotzdem recht wesentlich voneinander, denn die Werte der ersten Grundgesamtheit liegen viel weiter auseinander als die Werte der zweiten. Um diesen Unterschied zu erfassen, braucht man noch eine weitere Masszahl. Geeignet ist hierzu eine Zahl, die die Abweichung der Werte x1, … xn vom Mittelwert /x misst.
    Die gebräuchlichsten Streuungsmasse sind die Varianz S2 und die Standardabweichung s. Sie haben sich am stärksten durchgesetzt, weil sie eng mit dem arithmetischen Mittel verbunden sind, und weil sie als Schätzwerte gut verwendet werden können.
    Weiter wird noch unterschieden, ob sich die Werte aus der Grundgesamtheit oder aus einer Stichprobe berechnen. Von einer Grundgesamtheit sprechen wir, wenn die Zahlenreihe alle vorkommenden Werte umfasst. In der Statistik hat man häufig aber nur Stichproben, da man aus ökonomischen und/oder zeitlichen Gründen z.B. bei einer Meinungsumfrage nur einen Teil der Bevölkerung befragen kann. Mit mathematischen Methoden extrapoliert man dann diese Werte einer Stichprobe auf die ganze Bevölkerung. Die Funktionen zum Berechnen der Varianz und der Standardabweichung unterscheiden sich darum wie folgt:

    Grundgesamtheit: Excel-Befehl → STABWN (Alle Werte liegen vor)
    Stichprobe: Excel-Befehl → STABW (Mit der Stichprobe soll eine Aussagen bezüglich der Grundgesamtheit gemacht werden)

    Die Varianz einer Grundgesamtheit S2 wird durch folgende Formel definiert: Die Varianz S2 ist stets grösser oder gleich 0. Nimmt sie den Wert Null an, so heisst das, dass überhaupt keine Streuung vorliegt, d.h. alle Einzelwerte einander gleich sind und somit mit ihrem arithmetischen Mittelwert übereinstimmen.

  • Die Standardabweichung
    Die Varianz S2 ist in der theoretischen Statistik von grosser Bedeutung. In der betrieblichen Statistik hingegen treten oft Schwierigkeiten bei der Interpretation der quadrierten Ergebnisse auf. Um diese Interpretationsprobleme zu umgehen, wird oft die Standardabweichung (mittlere quadratische Abweichung) angegeben. Die Standardabweichung ist die Quadratwurzel aus der Varianz: Im folgenden Würfelbeispiel beträgt die Standardabweichung (aus der Stichprobe) bezogen auf den Mittelwert 1.94
    Der «Wahre Wert» liegt also mit sehr hoher Wahrscheinlichkeit im Bereich zwischen 2.29 und 4.24, was mit 3.5 auch zutrifft!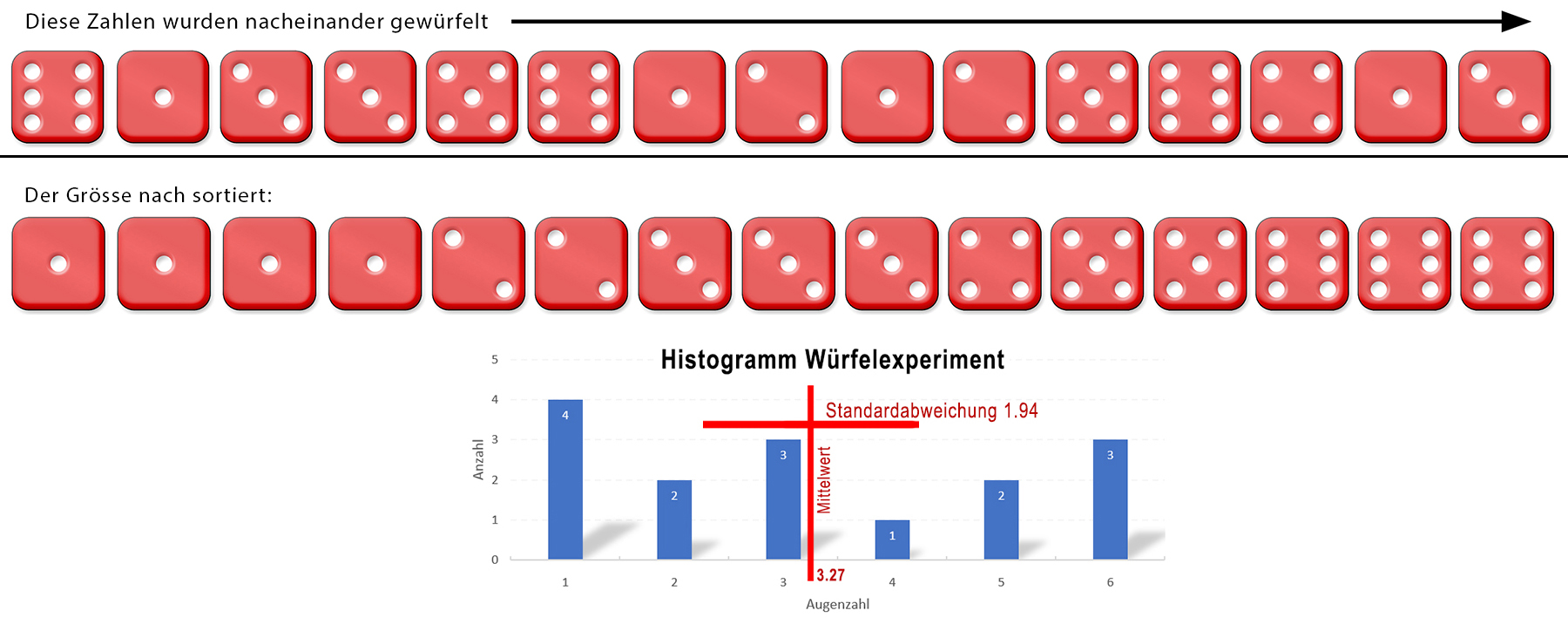

3.10 Excel und Logik

Auch in Excel ist es möglich, logische Auswertungen zu erstellen. Zwei Dinge sollen hier genannt werden:

  • IF/WENN: Selektion-Konstrukt → WENN(Zu prüfende Bedingung; Was tun, wenn erfüllt; Was tun, wenn nicht_erfüllt
  • AND/UND: Verknüpfungsoperator → falsch UND falsch = falsch, falsch UND wahr = falsch, wahr UND wahr = wahr
  • OR/ODER: Verknüpfungsoperator → falsch UND falsch = falsch, falsch UND wahr = wahr, wahr UND wahr = wahr
Beispiel: Erklärung zu der EXCEL-Funktion:
WENN(UND(B2>8;C2>1);"Ja";"NEIN") → WENN(Bedingung12;true-case;false-case)
Bedingung12 → UND(B2>8;C2>1) → UND(Bedingung1;Bedingung2)
Diese EXCEL-Datei herunterladen


Praxisaufgabe ∇ AUFGABEN
∇ LÖSUNGEN