Datenkompression

1. Einführung

Warum komprimieren?

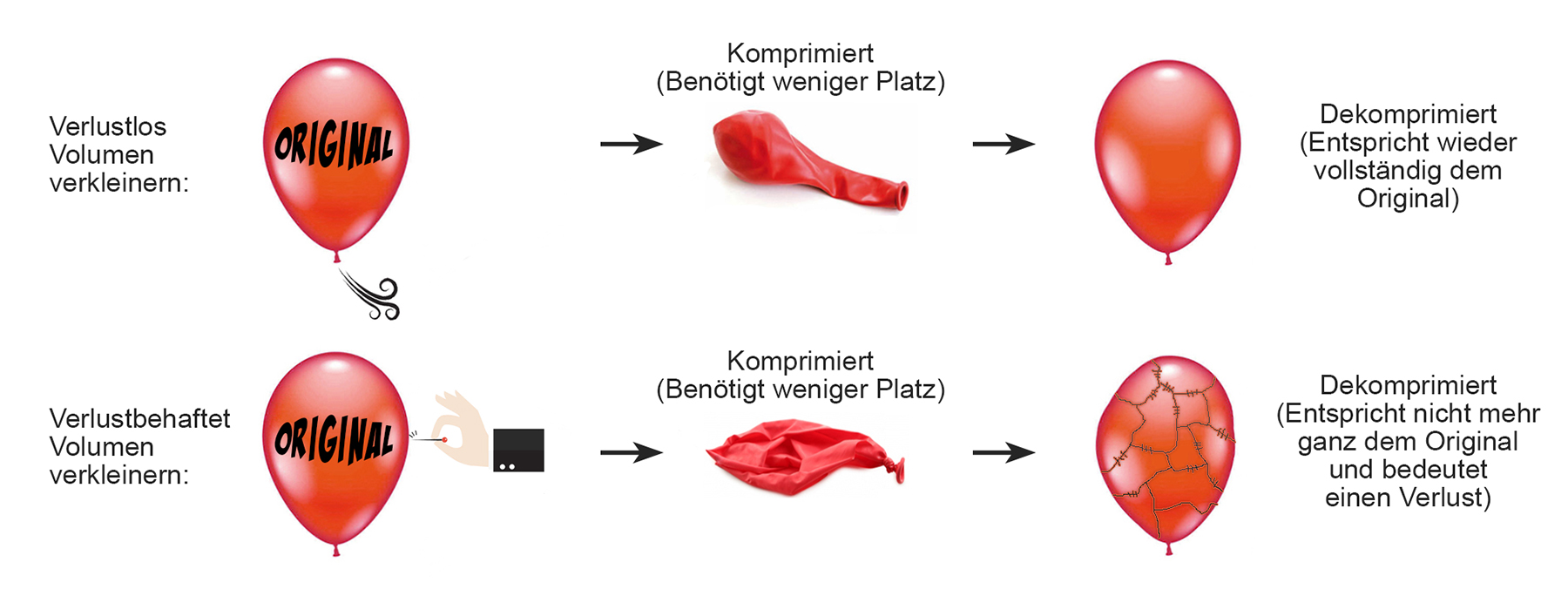
Grundsätzlich wird bei der Datenkompression versucht, redundante Informationen zu entfernen. Dazu werden die Daten in eine Darstellung überführt, mit der sich Informationen in kürzerer Form darstellen lassen. Diesen Vorgang übernimmt ein Kodierer und man bezeichnet den Vorgang als Kompression oder Komprimierung. Die Umkehrung bezeichnet man als Dekompression oder Dekomprimierung. Man spricht von verlustfreier Kompression, wenn aus den komprimierten Daten wieder alle Originaldaten gewonnen werden können. Das ist beispielsweise bei der Kompression ausführbarer Programmdateien notwendig. Bei der verlustbehafteten Kompression können die Originaldaten aus den komprimierten Daten meist nicht mehr exakt zurückgewonnen werden, das heisst, ein Teil der Information geht verloren. Solche Verfahren werden häufig zur Bild- oder Videokompression und Audiodatenkompression eingesetzt. Im folgenden werden die verlustlosen Komprimierungsverfahren behandelt. Verlustbehaftete Verfahren findet man im Multimediakurs unter Bild & Videotechnik. Dort findet man die DCT (Discrete Cosine Transformation) und Interframe-Komprimierungsverfahren.

2. VLC (Variable Length Code)

2.1 Der Morsecode

Der Morsecode, erfunden um 1838 von Samuel Morse und Alfred Lewis Vail, ist ein Verfahren, um in Seefunk und Telegrafie elektrisch, optisch oder akustisch verlustlos komprimiert Buchstaben, Zahlen und weitere Zeichen zu übermitteln. Die Codes haben unterschiedliche Codelängen (Variable Length Code). Häufig verwendete Zeichen erhalten einen kurzen Code, seltene einen langen:

Die Nachteile des Morsecodes:

Betrachtet man das folgende Beispiel, zeigt sich ein nicht unwesentlicher Nachteil dieses Verfahrens:
Was kann diese Codesequenz alles bedeuten:
« • • – • • • • – »?

• Vielleicht IDEA?     • •     – • •     •     • –
• oder doch USA?     • • –     • • •     • –
• Und falls UHT (UltraHighTemperatur) gemeint ist?     • • –     • • • •     –
• Und ginge nicht auch noch FV (FussballVerein)?     • • – •     • • • –

2.2 Die Huffman-Kodierung

Die Huffman-Kodierung ist eine Form der Entropiekodierung. Sie ordnet einer festen Anzahl an Quellsymbolen jeweils Codewörter mit variabler Länge zu. Der Huffman-Code ist ebenfalls ein VLC (Variable Length Code)

Die Huffman-Kodierung am Textbeispiel «ERDBEERE» erklärt:

Das Wort «ERDBEERE» zählt 8 Buchstaben. Zuerst soll die Häufigkeit der einzelnen Buchstaben ermittelt werden: Danach erstellt man einen binären Baum: Die am wenigsten häufigen Buchstaben werden zu einem übergeordneten Knoten zusammengefasst Und so geht das entsprechend weiter bis man zuoberst beim letzte Knoten angelegt ist. Dieser schliesst den Aufbau des Baums ab. Die Wertigkeit des obersten Knotens, in diesem Fall die Zahl 8, muss der Summe aller Buchstaben des codierten Worts (hier «ERDBEERE») entsprechen. 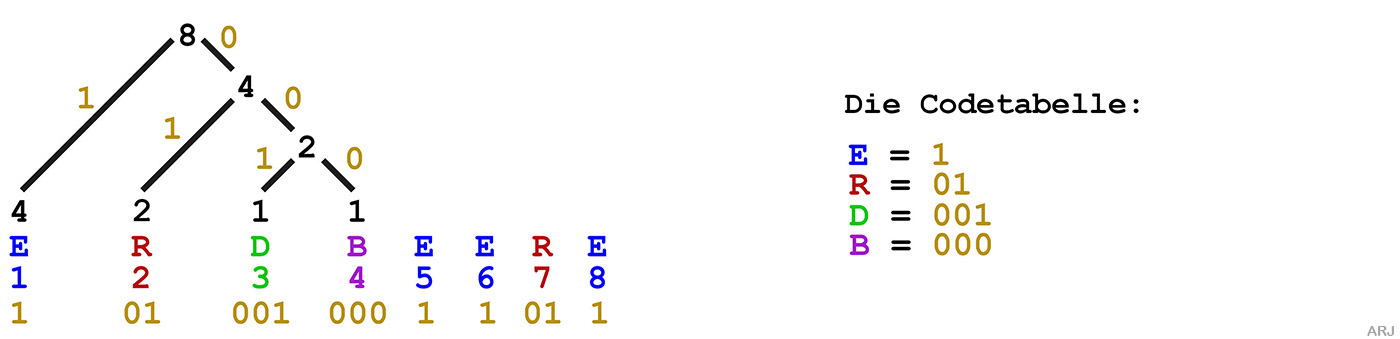Jetzt müssen die Äste des Baums beschriften werden - Nach Links 1 und nach Rechts 0 (Nach Links 0 und nach Rechts 1 wäre auch möglich) Somit hat man den Huffman-Code für das Wort «ERDBEERE» ermittelt. (Mit nur 14 Bit ein Leichtgewicht gegenüber dem Wort «ERDBEERE» als ASCII-Text mit 8 x 8Bit (=64Bit) Beim vorangegangenen Beispiel ist nur eine Lösung möglich. Das ändert sich, wenn man der ERDBEERE ein N anhängt, also ERDBEEREN daraus macht.

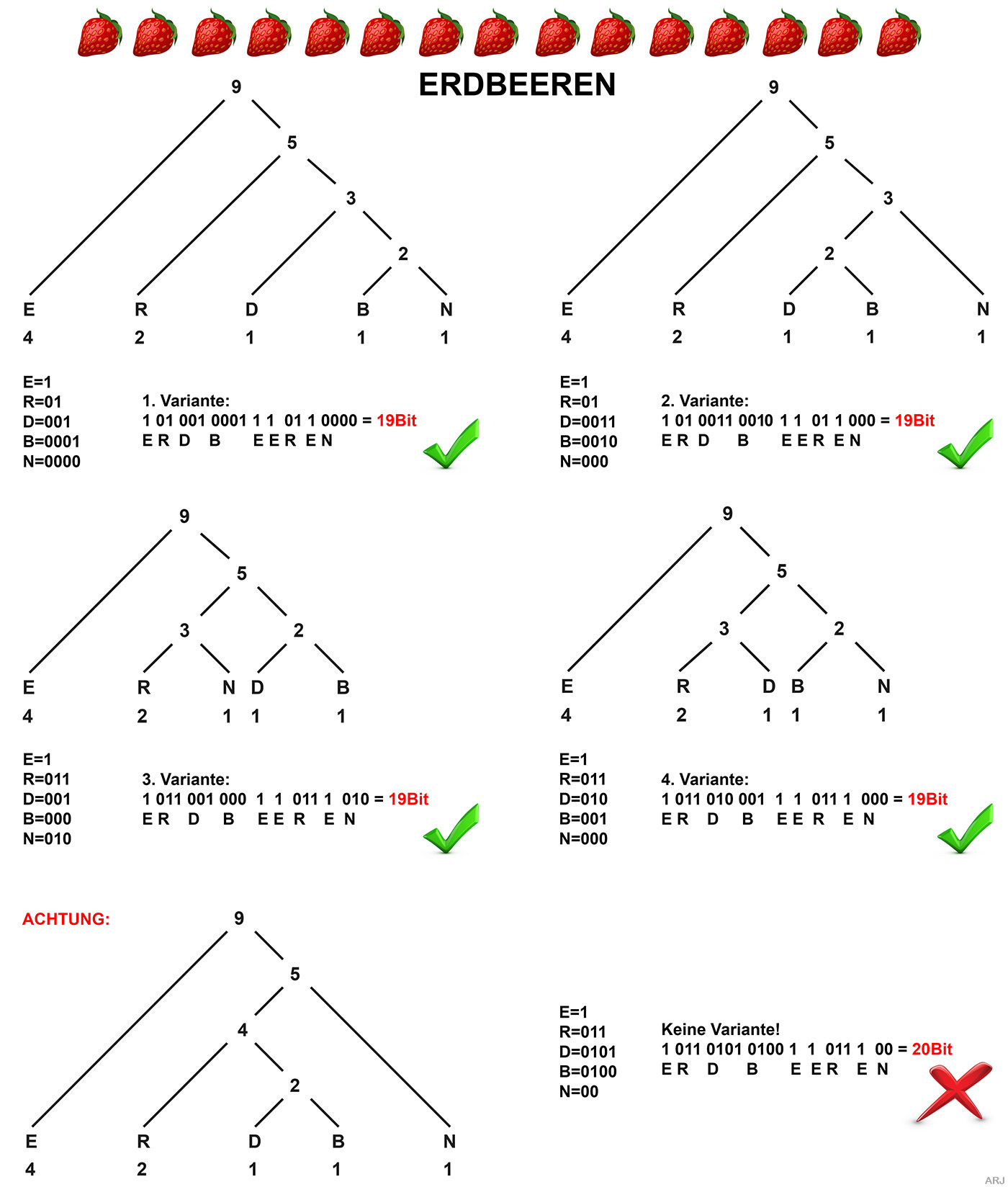
Fallbeispiel «ERDBEEREN»:

Mehrere Lösungen sind nun möglich. Allerdings führen alle zur selben Codeeffizienz. (Das letzte Beispiel zeigt ein falscher Aufbau des binären Baums.)

3. RLC (Run Length Coding)

Mit Run Length Coding (bzw. RLE → Run Length Encoding) ist eine Lauflängenkodierung gemeint. Jede Sequenz von identischen Symbolen soll durch deren Anzahl und ggf. das Symbol ersetzt werden. Somit werden nur die Stellen markiert, an denen sich das Symbol in der Nachricht ändert. Effizient bei langen Wiederholungen. 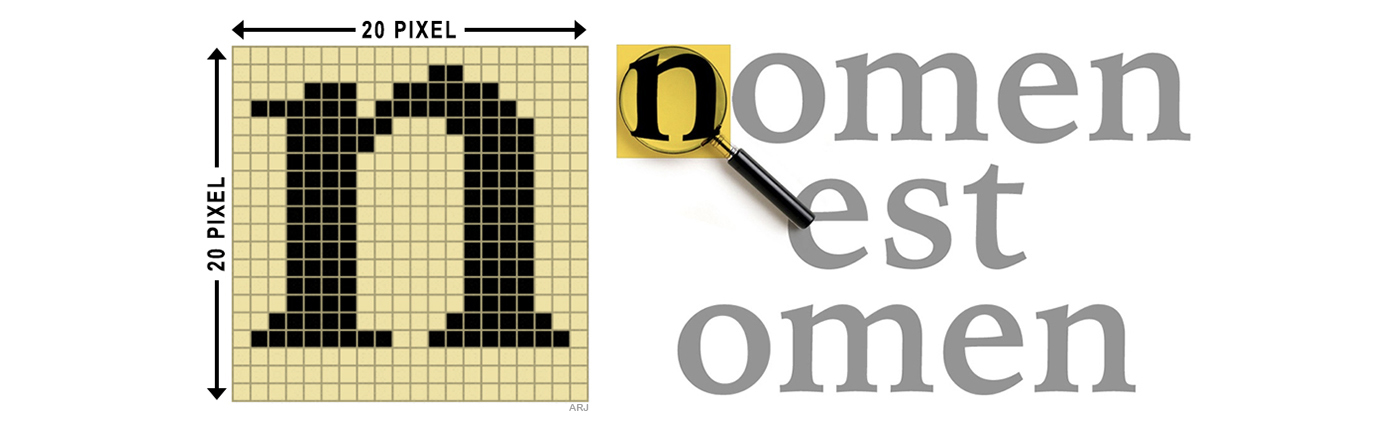RLE-Bit-Berechnung für die ersten vier Zeilen:

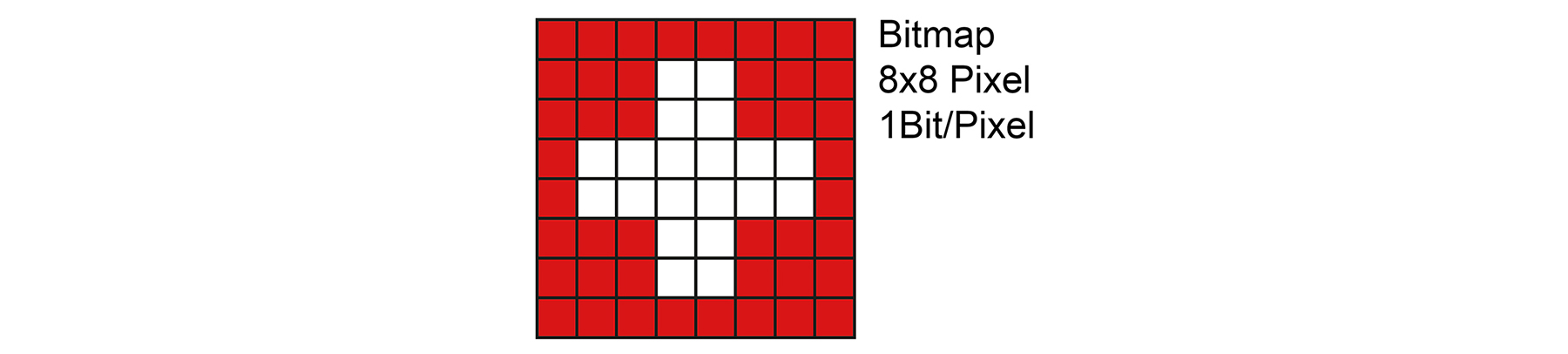
• Der Speicherbedarf für das RLC-komprimierte Bild:
  Ab erstem Pixel oben links: 31 x Weiss, 2 x Schwarz, 11 x Weiss, 3 x Schwarz, 2 x Weiss, 6 x Schwarz, 6 x Weiss, 6 x Schwarz, 1 x Weiss, 8 x Schwarz, 4 x Weiss
  Total: 11 Zahlen oder Farbwechsel. Grösste Zahl: 31 (Benötigt 5 Bit)
  Die Zahlen im Binärcode: 11111 - 00010 - 01011 - 00011 - 00010 - 00110 - 00110 - 00001 - 01000 - 00100
  Zusammenfassend RLC: 11 x 5Bit = 55Bit (Der Abstand mit Bindestrich wurde nur zwecks besserer Lesbarkeit hinzugefügt.)
• Der Speicherbedarf für das normale Bitmap: 4 Zeilen zu je 20 Pixel = 80Bit

Ein paar Gedanken zu Huffman und RLC

Am Beispiel «A N A N A S» soll überlegt werden, was Huffman gegenüber unkomprimiertem ASCII ergibt und ob man mit z.B. RLC noch ein paar Bit "herausquetschen" kann. 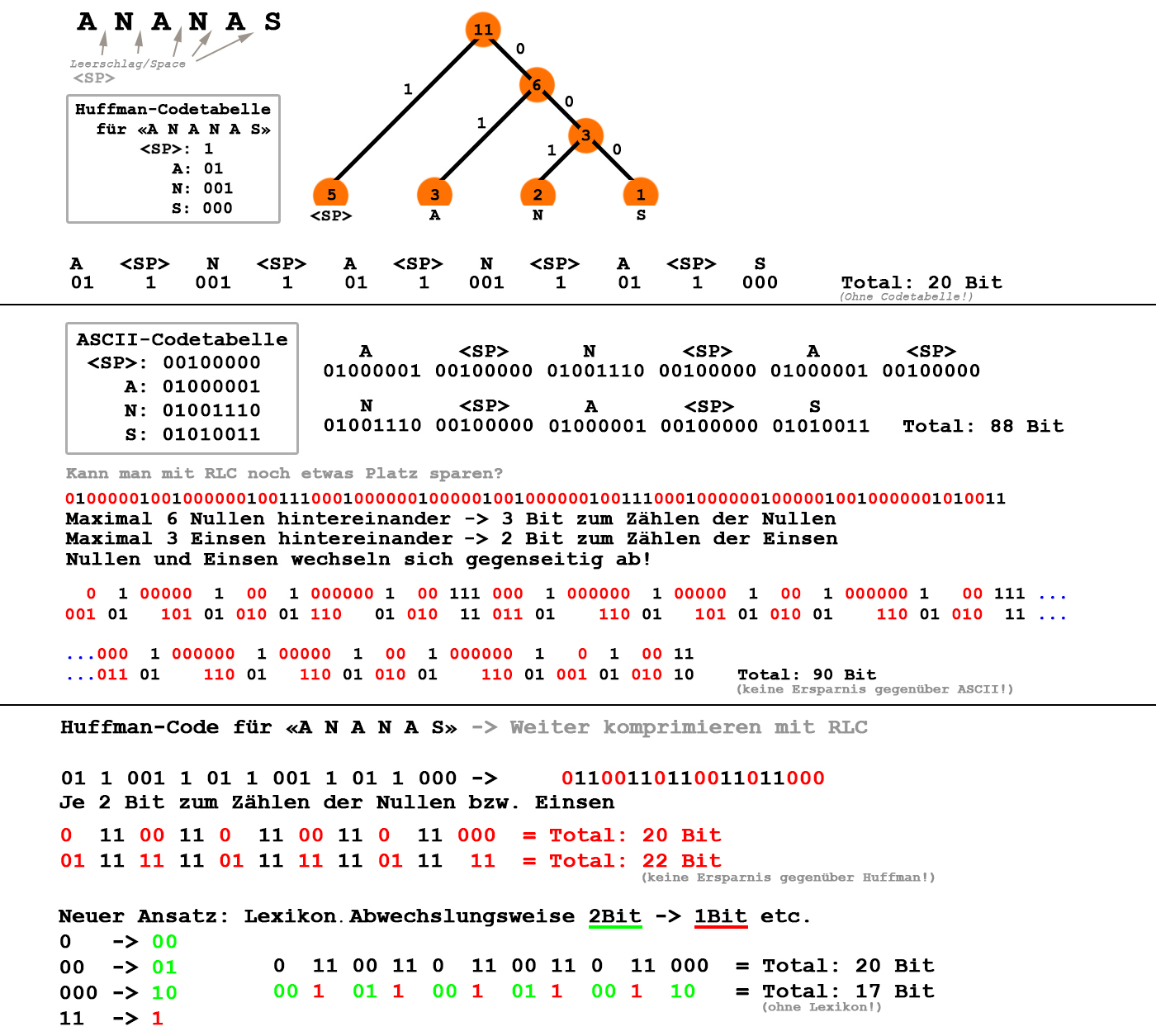Die Erkenntnis: Es ist zu prüfen, ob allenfalls eine Kombination von verscheidenen Verfahren eine noch höhere Datenreduktion ergeben kann.

4. LZW (Lempel-Ziv-Welch)

Ein anderer Ansatz verfolgt der Lempel-Ziv-Welch-Algorithmus: Die Idee dahinter ist, wiederkehrende binäre Muster nicht erneut zu speichern, sondern eine Reeferenz darauf. Es wird eine Art Wörterbuch erstellt. LZW wird häufig bei der Datenreduktion von Grafikformaten (GIF, TIFF) verwendet.

LZW-Transformation am Textbeispiel «ENTGEGENGENOMMEN» erklärt:

Das Wort «ENTGEGENGENOMMEN» soll verlustlos datenreduziert bzw. komprimiert werden. Die Werte 0 bis 255 sind den ASCII-Zeichen vorbehalten. Die Werte ab 256 sind Indexe, die auf einen Wörterbucheintrag verweisen:

LZW-Rücktransformation:

Die bisher vorgestellten Verfahren Huffman, RLC und LZW bewirken alle direkt eine verlustlose Datenreduktion. Es gibt aber auch Verfahren, die Daten nicht selber komprimieren, sondern diese in eine für die spätere Komprimierung günstige Anordnung bringen. Der nächste Algorithmus BWT, wie auch die in Multimedia/Bild & Videotechnik gezeigte DCT (Discrete Cosine Transformation) verfolgen genau dieses Ziel. Beide verwenden schlussendlich VLC und/oder RLC für die eigentliche Komprimierung.

5. BWT (Burrows-Wheeler-Transformation)

Neben RLC, Huffman und LZW ist BWT eine weitere Art, wie Daten verlustlos komprimiert werden können. BWT ist allerdings kein Algorithmus, der Daten direkt komprimiert. Vielmehr besteht seine Aufgabe darin, das Datenmaterial für eine anschliessende effektive Datenreduktion mit z.B. RLC vorzubereiten.

BW-Transformation am Textbeispiel «ERDBEERE» erklärt:

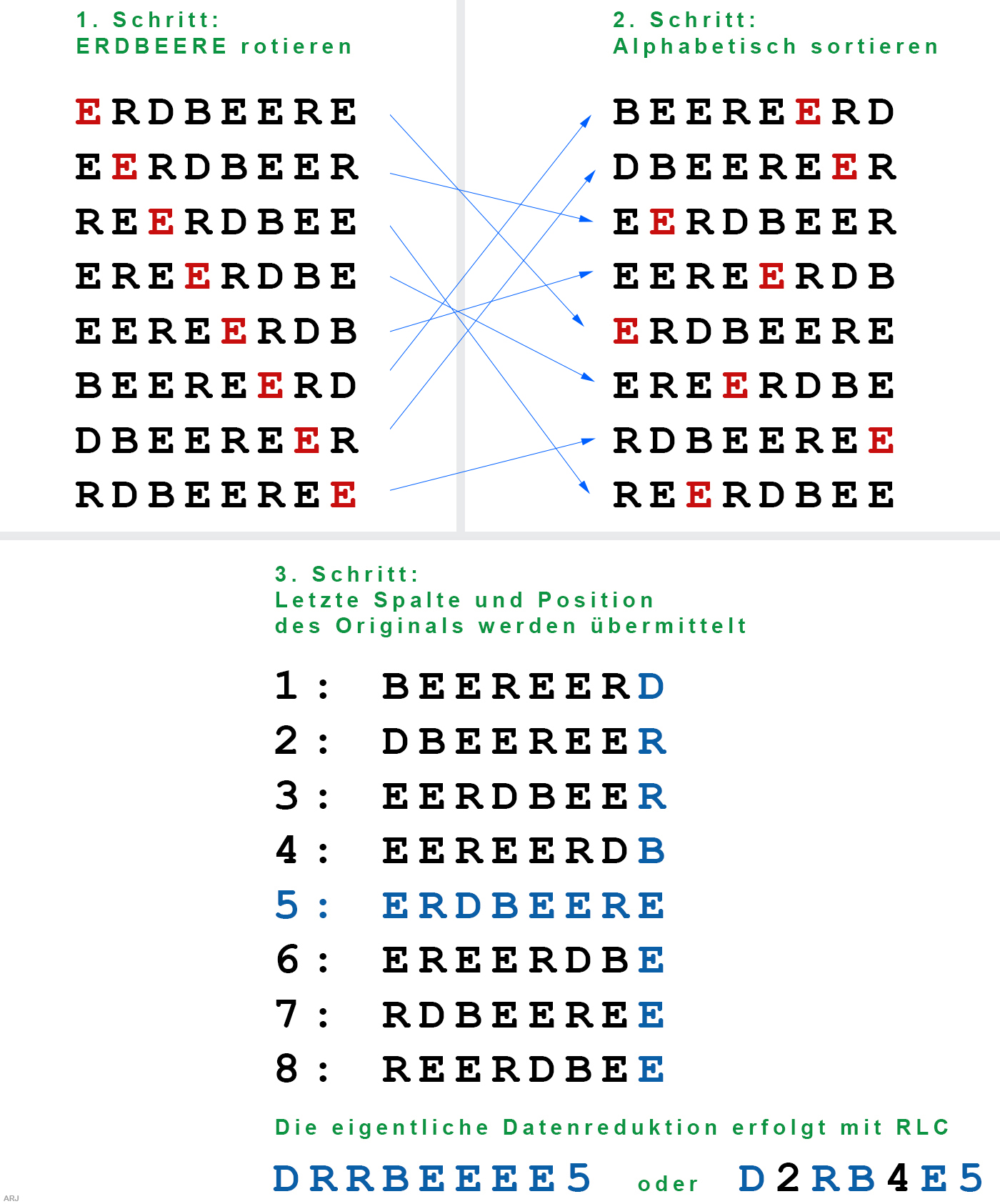
Die BW-Rücktransformation:

Die verlustbehafteten Komprimierungsverfahren werden im Kurs Multimedia/Bild & Videotechnik behandelt!