Ausgewählte Digitaltechnikthemen

1. Einführung

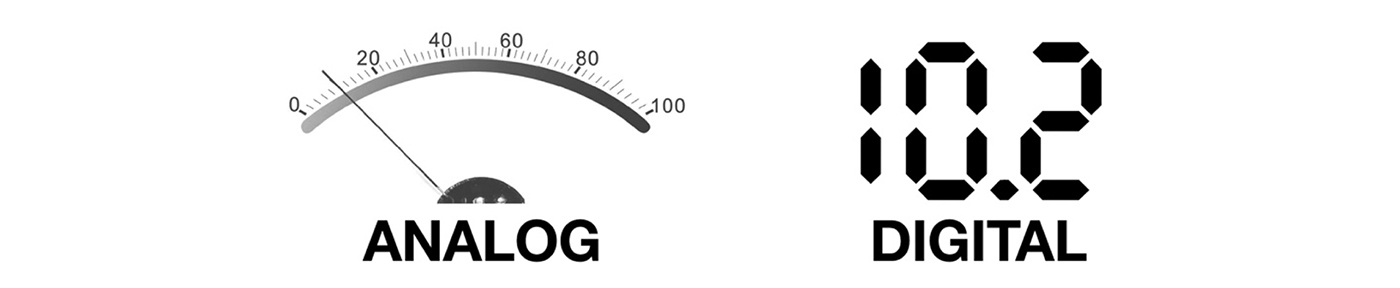
Analog und Digital

Der Unterschied Analog zu Digital aufgezeigt an einem Messinstrument:

• Ein Vorteil der analogen Anzeige besteht darin, dass innerhalb des Anzeigebereichs viele beliebige Werte kontinuierlich angezeigt werden können.
• Ein Nachteil der analogen Anzeige ist aber, dass Werte je nach Sicht auf die Zeigernadel, ungenau abgelesen werden. (Ablesefehler)
• Für eine digitale Anzeige spricht, dass keine Ablesefehler gemacht werden können.
• Allerdings werden bei der digitalen Anzeige die Werte nicht kontinuierlich, sondern zeitdiskret angezeigt. Je nach Samplingrate kann da ein kurzer Ausschlag übersehen werden. Ausserdem können bei obiger digitaler Anzeige nur Werte von 00.0 bis 99.9, also 1000 verschiedene Werte, angezeigt werden.

Bit und Byte

Der Begriff Bit (engl. Binary Digit) dient als Masseinheit für die Datenmenge digital gespeicherter oder übertragener Daten. Der Computer kennt nur 0 und 1. Das bedeutet soviel wie «Strom ein», «Strom aus». Das heisst, dass die Daten in der PC-Elektronik binär verarbeitet werden. Ein guter Grund also, sich mit dem Binärsystem oder 2-er System auseinanderzusetzen. In der Informatik ebenfalls wichig ist das Hexadezimalsystem oder 16-er System, weil z.B. Speicheradressen in Hex angegeben werden, aber auch MAC-Adressen oder sogar die neuen IPv6-Adressen.

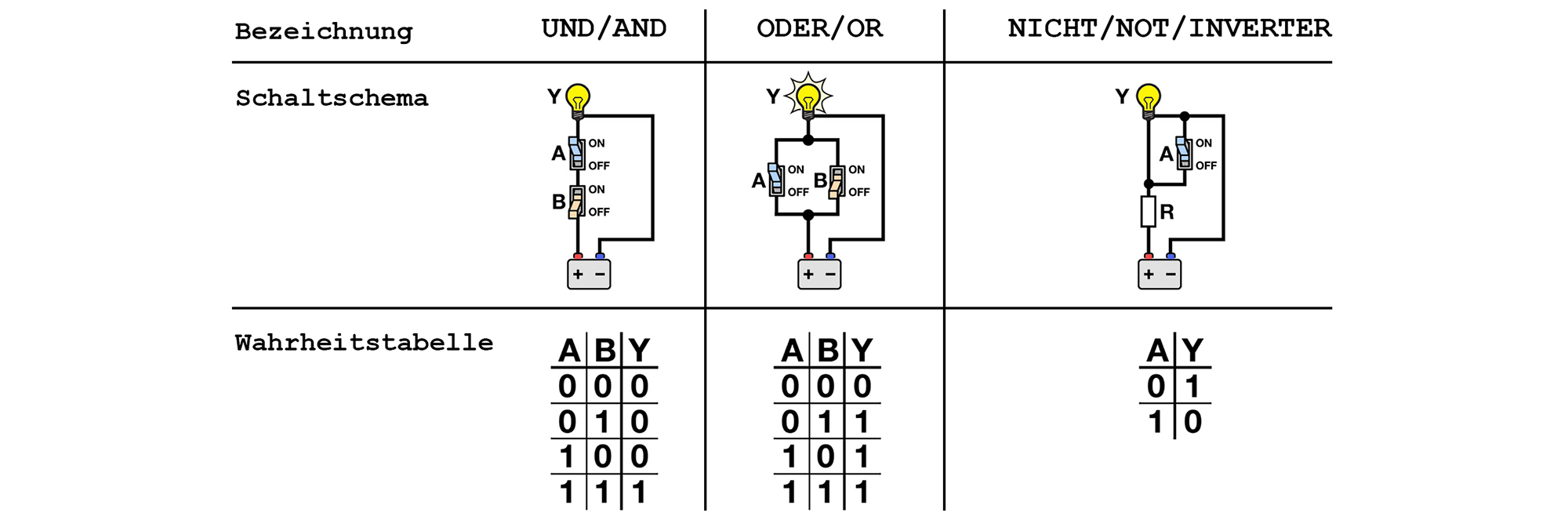
• 1 bedeutet: Logisch WAHR oder TRUE / eine Spannung vorhanden / Licht an / On / Schalter geschlossen
• 0 bedeutet: Logisch FALSCH oder FALSE / keine Spannung vorhanden / Licht aus / Off / Schalter offen

• Kleiner als 1 Bit geht nicht! (z.B. existiert kein 1/2 Bit)
• Das Kurzzeichen für Byte ist das grosse «B» (z.B. 100MB)
• Das Kurzzeichen für Bit ist das kleine «b» (z.B. 100b)
• 1 Byte beinhaltet 8 Bit
• 1 Byte entspricht zwei HEX-Ziffern (z.B. 1011'0100 = B4)
• 1 Byte hat 256 Bitkombinationen
• Speichergrössen von z.B. SSD's oder Harddisks werden üblicherweise in Byte angegeben (z.B. 1TB) Siehe auch IEC-Präfixe.
• Datenübertragungsraten von z.B. Modems werden üblicherweise in Bit/Sekunde angegeben (z.B. 800kb/sec)

Kombinatorik

Mit Kombinatorik ist die Verknüpfung zweier Aussagen oder Aussagefunktionen gemeint, wie wir dieser auch bei der Programmierung begegnen.

Information in digitaler Form

Jede Datei besteht schlussendlich "nur" aus Bit und Bytes → Welche Information verbirgt sich aber dahinter? Der Computer speichert allerlei Daten. Ob Tabellen, Briefe, Programme, Bild, Ton oder gar Videos, es sind immer Bit’s und Byte’s, um die es sich handelt und die entsprechende Applikation muss wissen, wie sie mit diesen umzugehen hat. Beispiele von Dateiarten:

• Vektorgrafik: EPS/SVG/DXF
• Bitmapbild bzw. Rastergrafik: JPG/GIF/TIF
• ASCII- oder Unicodetext
• Audio & Video: MPEG2/MPEG4
• EXCEL-Tabellenkalkulation: XLS
• Ausführbares Programme: EXE-Datei
• PortableDocumentFormat: PDF
• Webseite: HTML, CSS
• Microsoft WORD Dokument: DOC
• und viele weitere.

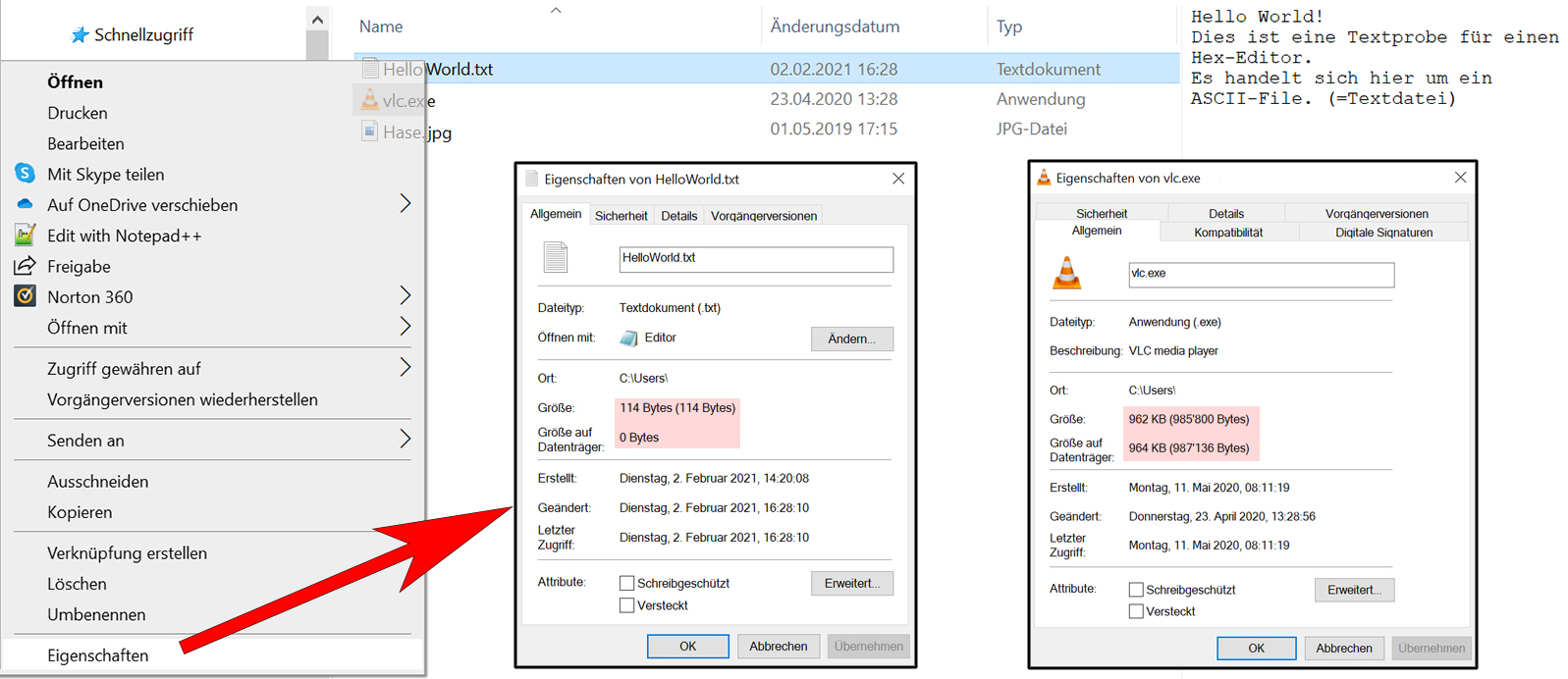
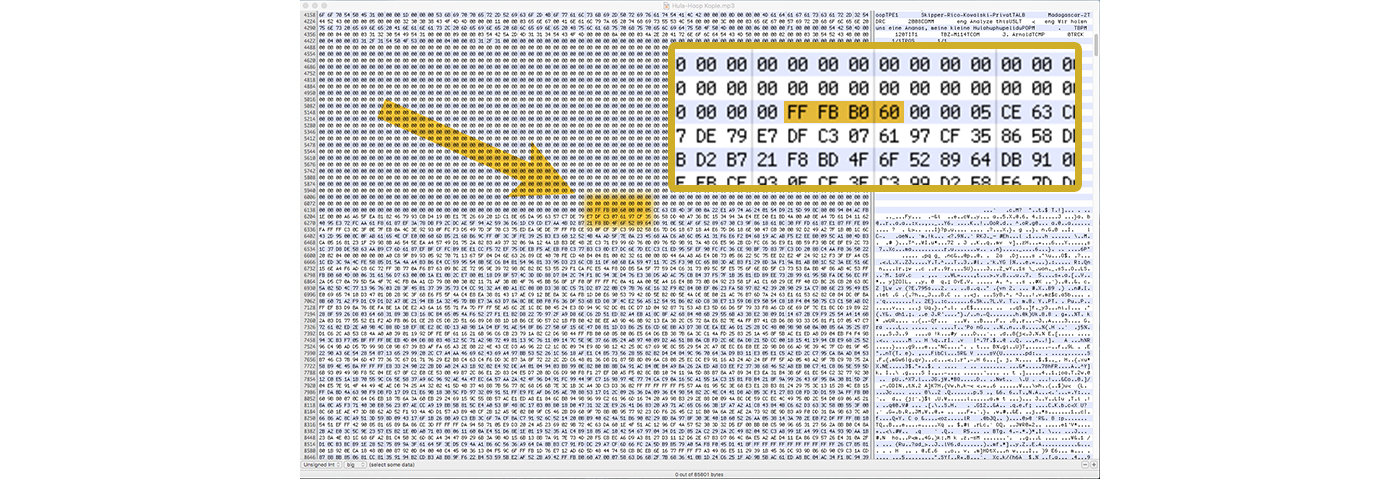
Der Hex-Editor (Applikation)

Manchmal möchte man sich eine Datei binär anzeigen lassen und vielleicht auch eine Änderung vornehmen, wobei man dann ganz genau wissen muss, was man wo hinzufügt oder wegnimmt. In solchen Fällen kann ein Hex-Editor weiterhelfen. Der Hex-Editor stellt eine ausgewählte Datei so dar:

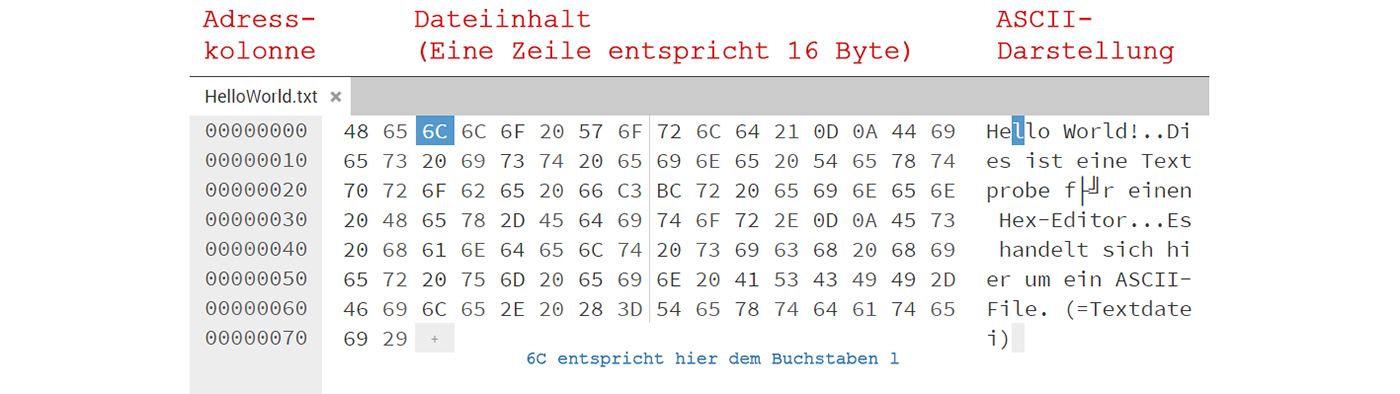
• Erste Kolonne: Adresse des ersten Bytes der entsprechenden Zeile in hexadezimaler Darstellung.
• Zweite Kolonne: 16 Daten-Bytes. Pro Byte zwei Hex-Ziffern.
• Dritte Kolonne: Den Versuch die 16 Bytes als ASCII-Character darzustellen. (Was in diesem Beispiel gelingt. Bei einer nicht als Textdatei interpretierbaren JPG-Bilddatei würde dies scheitern. Probieren sie es aus!)

2. Massvorsätze

2.1 SI-Präfixe

Mit SI-Präfixe («Système international d’unités») sind Massvorsätze gemeint. Diese wenden wird ganz selbstverständlich auf z.B. Basisgrössen wie Länge in Kilometer «km» oder Masse in Kilogramm «kg» an. Diese Präfixe kommen allerdings auch in der Informatik vor, wie z.B. bei «MB/s» für Megabyte pro Sekunde oder «kb/s» für Kilobit pro Sekunde. Wenn also eine Sache «MegaCool» ist, heisst das, dass sie eine Million Mal «Cooler» ist als nur «Cool».

• [Y] → Yotta → 10²⁴ → 1'000'000'000'000'000'000'000'000 → Quadrillion
• [Z] → Zetta → 10²¹ → 1'000'000'000'000'000'000'000 → Trilliarde
• [E] → Exa → 10¹⁸ → 1'000'000'000'000'000'000 → Trillion
• [P] → Peta → 10¹⁵ → 1'000'000'000'000'000 → Billiarde
• [T] → Tera → 10¹² → 1'000'000'000'000 → Billion
• [G] → Giga → 10⁹ → 1'000'000'000 → Milliarde
• [M] → Mega → 10⁶ → 1'000'000 → Million
• [k] → kilo → 10³ → 1'000 → Tausend
• [-] → 10⁰ → 1 → Eins
• [m] → milli → 10^-3 → 0.001 → Tausendstel
• [µ] → mikro → 10^-6 → 0.000'001 → Millionstel
• [n] → nano → 10^-9 → 0.000'000'001 → Milliardstel
• [p] → piko → 10^-12 → 0.000'000'000'001 → Billionstel
• [f] → femto → 10^-15 → 0.000'000'000'000'001 → Billiardstel
• [a] → atto → 10^-18 → 0.000'000'000'000'000'001 → Trillionstel

• 1km = 1‘000 Meter
• 1kg =1‘000 Gramm
• 1kb = 1‘000 Bit (kleines b!!!)
• 1MB = 1‘000‘000 Byte (grosses B!!)
• Übrigens: 1Byte entspricht 8 Bit (1B = 8b)

2.2 IEC-Präfixe

Die folgenden IEC-Präfixe «International Electrotechnical Commission» werden für Kapazitätsangaben bei Speichermedien verwendet. Grund: Für Datenspeicher mit binärer Adressierung ergeben sich Speicherkapazitäten von 2ⁿ Byte, d. h. Zweierpotenzen.

• [Yi] → Yobi → 2⁸⁰ → 1'208'925'819'614'629'174'706'176
• [Zi] → Zebi → 2⁷⁰ → 1'180'591'620'717'411'303'424
• [Ei] → Exbi → 2⁶⁰ → 1'152'921'504'606'846'976
• [Pi] → Pebi → 2⁵⁰ → 1'125'899'906'842'624
• [Ti] → Tebi → 2⁴⁰ → 1'099'511'627'776
• [Gi] → Gibi → 2³⁰ → 1'073'741'824
• [Mi] → Mebi → 2²⁰ → 1'048'576
• [Ki] → Kibi → 2¹⁰ → 1'024

• 1 MiB ist 1 Mebibyte oder 1'048'576 Byte
• 512 MiB (Mebibyte) = 512 * 2²⁰ Byte = 536'870'912 Byte
• 256 kib (Kibibit) = 256 * 2¹⁰ Bit = 262'144 Bit
• Übrigens: 1Byte entspricht 8 Bit (1B = 8b)

3. Zahlensysteme

Im Folgenden werden die für Informatiker wichtigsten positionellen bzw. Stellenwert-Zahlensysteme behandelt: 2-er, 10-er und 16-er System

Bei positionellen bzw. Stellenwert-Zahlensystemen gilt allgemein:

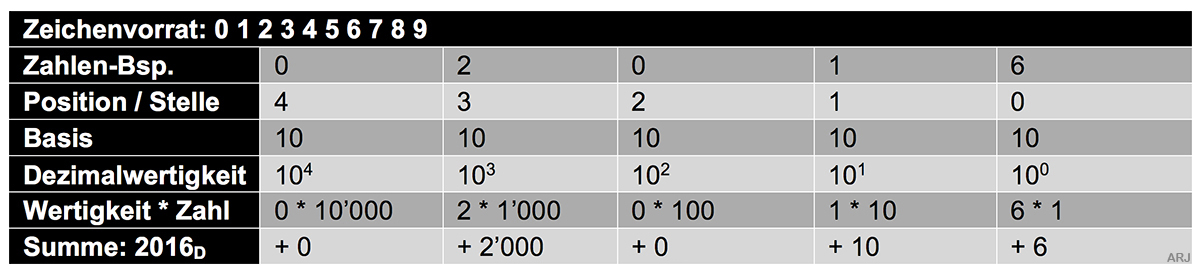
3.1 Das Dezimalsystem

Dieses Zahlensystem ist allseits bekannt. Darum knüpfen die folgenden Betrachtungen an diesem System an:
(Damit eine Dezimalzahl von einer Binär- oder Hexadezimalzahl unterschieden werden kann, soll sie am Ende mit einem tiefergestellten «D» (Tiefstellung/Subskript) gekennzeichnet werden. Bsp.: 5238_D, 1000_D

3.2 Das Binärsystem

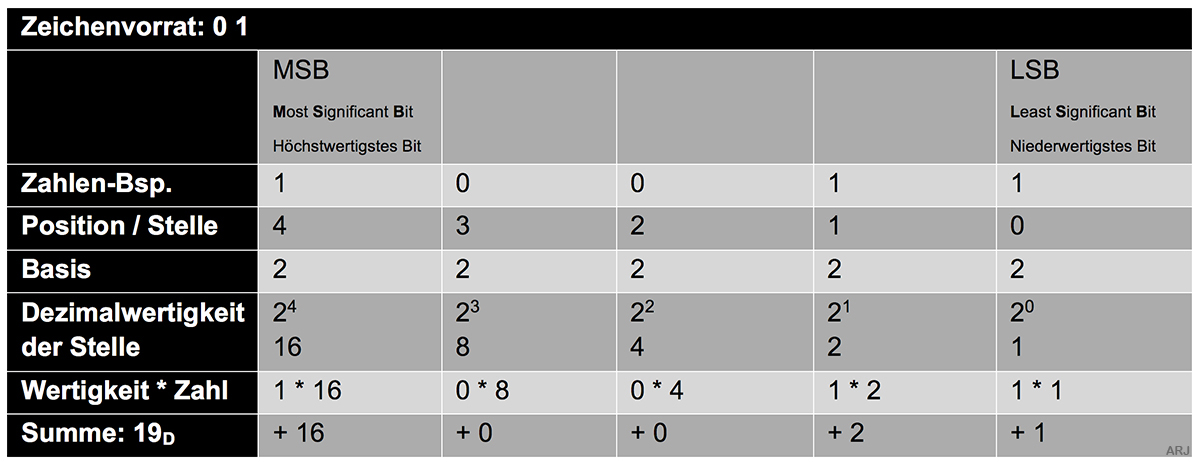
Das Binärsystem kennt nur die Ziffern 0 und 1. Im Gegensatz zum Dezimalsystem wo vorausgesetzt werden kann, dass die kleinstwertigste Ziffer immer rechts steht, trifft das bei Binärzahlen nicht immer zu, insbesondere bei Elektronik-Schaltplänen nicht. Darum sollte dies mit dem Zusatz LSB bzw. MSB geklärt werden.
(Damit eine Binärzahl von einer Dezimal- oder Hexadezimalzahl unterschieden werden kann, soll sie am Ende mit einer tiefergestellten «B» (Tiefstellung/Subskript) gekennzeichnet werden. Bsp.: 1101_B
In vielen Fällen werden sogenannte führende Nullen angegeben. Die Dezimalzahl 5_D sieht als 4-Bit-Zahl demzufolge so aus: 0101_B, als 8-Bit-Zahl: 0000'0101_B und als 16-Bit-Zahl: 0000'00000'0000'0101_B)

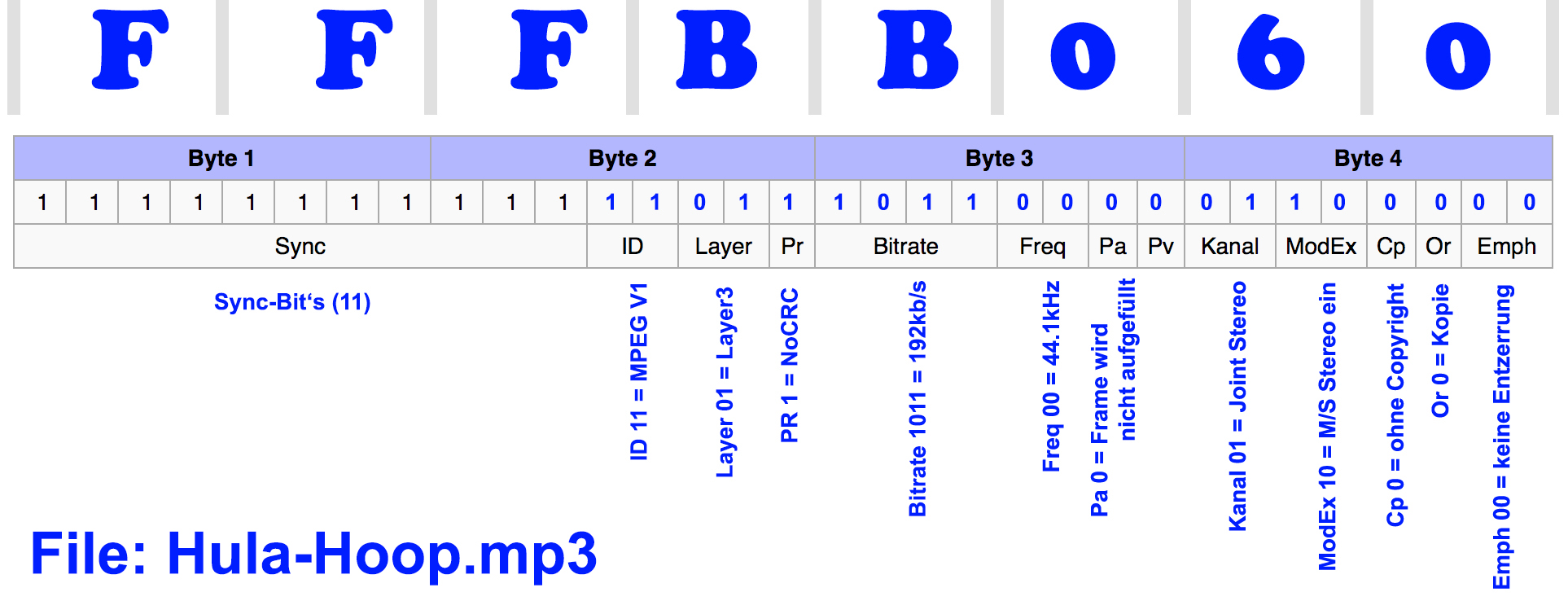
3.3 Das Hexadezimalsystem

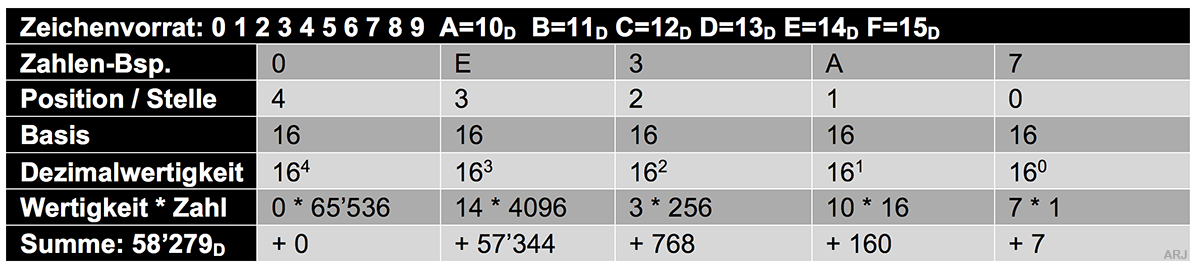
Das Hexadezimalsystem bedient sich für die ersten zehn Werte bei den Ziffern des Dezimalsystems. Für die weiteren sechs Werte benutzt man Ziffern des Alphabets.
Zahlen in hexadezimaler Schreibweise begegnet man z.B. in der Netzwerktechnik bei MAC- oder IPv6-Adressen oder bei der RAM-Speicheradressierung bzw. immer dann, wenn die binäre Schreibweise zu einem riesigen Zahlenkoloss führen würde. Stellen sie sich eine 128 Bit-IPv6-Adresse in binärer Schreibweise vor - also mit 128 Ziffern. Sie ist schon mit den 32 Ziffern in Hex lange genug.
(Damit eine Hexadezimalzahl von einer Binär- oder Dezimalzahl unterschieden werden kann, soll sie am Ende mit einer tiefergestellten «H» (Tiefstellung/Subskript) gekennzeichnet werden. Bsp.: 1A3B_H , 1426_H, 1001_H)

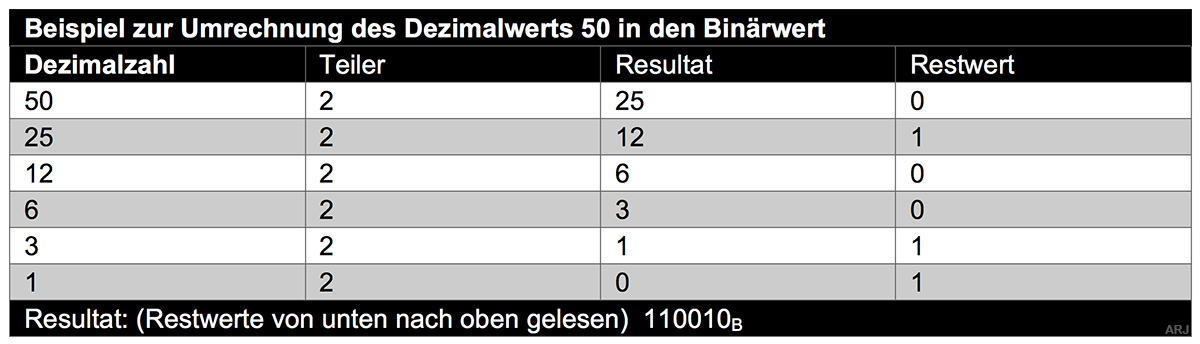
3.4 Die Fortlaufende Division

Wird verwendet zur Umrechnung von Dezimal zu Binär oder Dezimal zu Hexadezimal.

3.5 Umrechnung Hexadezimal zu Binär

• Binär > Hex: Binärzahl vom LSB in Richtung MSB in 4-er Gruppen unterteilen
• Hex > Binär: Eine Hex-Ziffer entsprechen 4 Bit’s

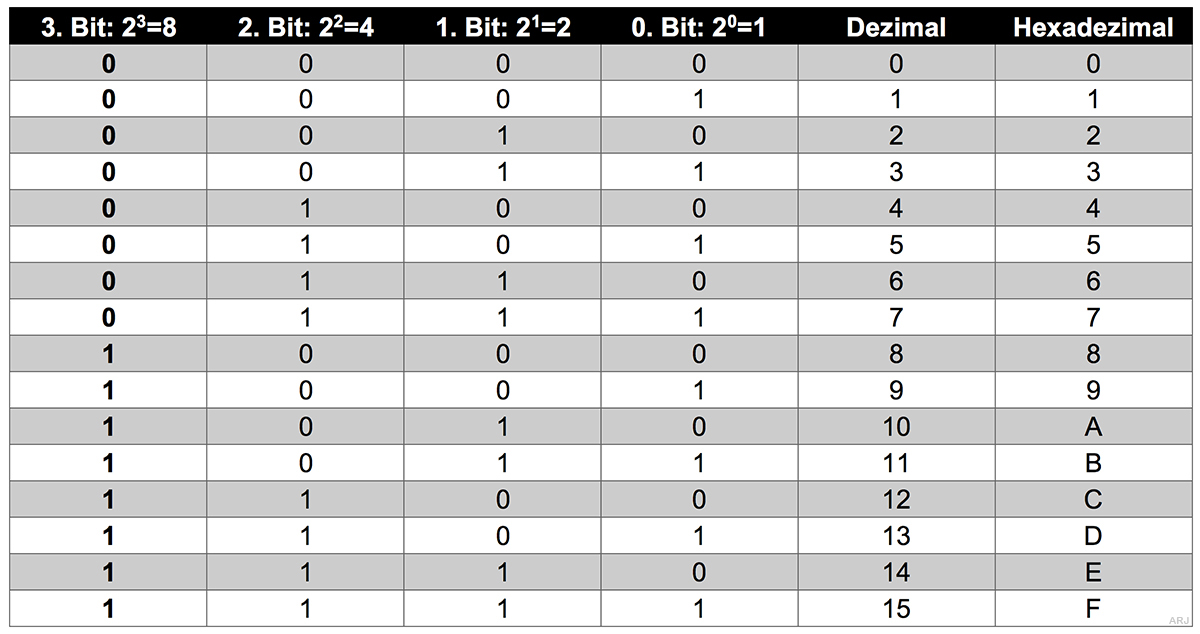
3.6 Die HEX-Tabelle

3.7 Die Anzahl Bit-Kombinationen ermitteln

Wie aus der folgenden Tabelle ersichtlich, verdoppelt sich die Anzahl Bitkombinationen mit jeder weiteren Bit-Stelle

• 1 Bit ergibt 2 Kombinationen (0 1)
• 2 Bit ergibt 4 Kombinationen (00 01 10 11)
• 3 Bit ergibt 8 Kombinationen (000 001 010 011 100 101 110 111)
• 4 Bit ergibt 16 Kombinationen (siehe obige Tabelle)
• 5 Bit ergibt 32 Kombinationen
• 6 Bit ergibt 64 Kombinationen
• 7 Bit ergibt 128 Kombinationen
• 8 Bit ergibt 256 Kombinationen
• ...

   Die Anzahl Kombinationen lassen sich mit der Formel berechnen:
   «Anzahl Bit-Kombinationen» = 2 «Anzahl Bitstellen»
   (Exponentialfunktion)

   Die Anzahl Bits lassen sich mit der Formel berechnen:
   «Anzahl Bit» = AUFRUNDEN(LOG «Anzahl Bit-Kombinationen» / LOG 2)
   (LOG = Zehnerlogarithmus)

3.8 Binäres Rechnen und Datenüberlauf

0 + 0 = 0
0 + 1 = 1
1 + 1 = 10 (Übertrag von 1 auf die nächsthöhere Stelle)
1 + 1 + 1 = 11 (Übertrag von 1 auf die nächsthöhere Stelle)

Beispiel Wertebereich von Integer:

Der Integer ist aktuell eine 32 Bit-Ganzzahl. (Früher 16 Bit)
2³² ergibt 4'294'967'296 Kombinationen.

Ein vorzeichenloser Integer (Unsigned Int) hat einen Wertebereich von 0 bis 4'294'967'295
Ein  normaler Integer mit Vorzeichen hat einen Wertebereich von -2'147'483'648 bis +2'147'483'647

3.9 Das 2-er Komplement - Negative Zahlen im Binärsystem

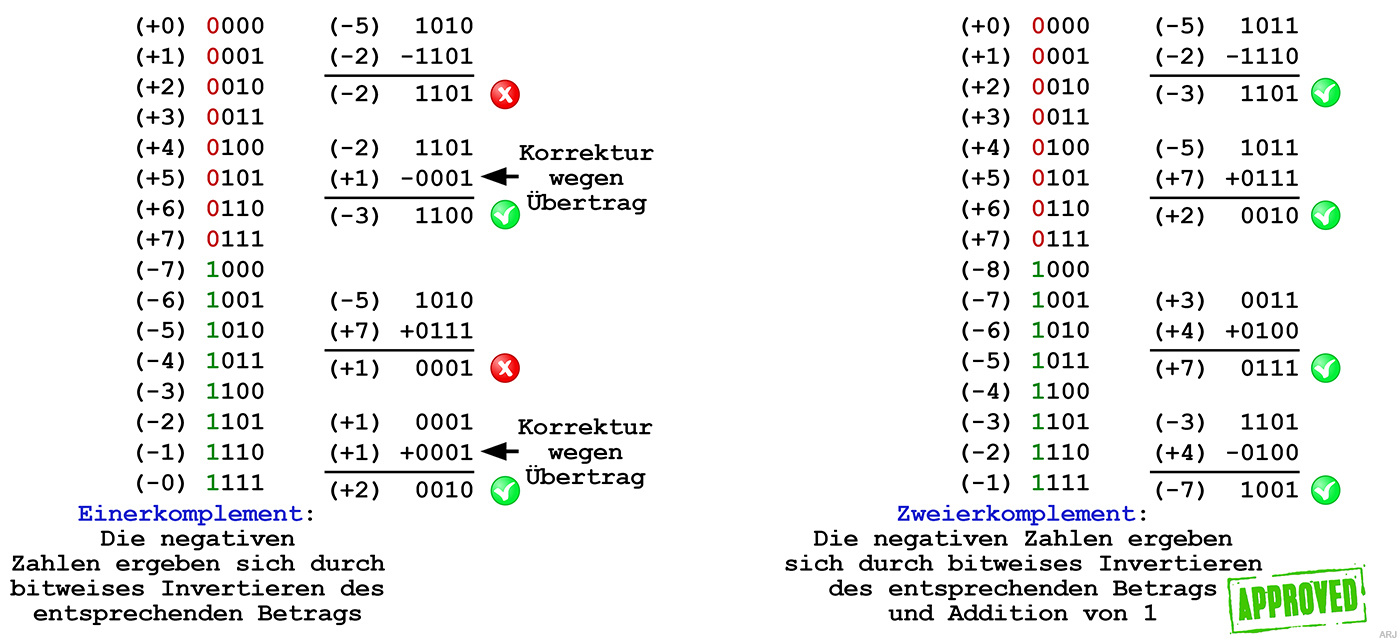
Bisher betrachtete wir nur den positiven Ganzzahlenbereich im Sinne von «Unsigned Integer». Schnell wird aber das Bedürfnis aufkommen, den Wertebereich in den negativen Zahlenbereich «Integer» zu erweitern. Dazu werden wir uns nun ein paar Gedanken machen. Wie wir nun gesehen haben, würde die Komplementbildung mit dem 1-er Komplement funktionieren, ausser es entsteht ein Übertrag oder eine Nulldurchschreitung. Mit einem Korrekturwert könnte dieser Mangel behoben werden. Allerdings bleibt der Nachteil, dass der Wert «0» zweimal vorhanden ist. Besser wird das 2-er Komplement funktionieren, wie wir nun sofort erkennen werden.

Zusammenfassung:

   Umwandlung einer negativen in eine positive Binärzahl oder umgekehrt:
   1. Invertiere alle Binärstellen
   2. Addiere 1
   
   Zahlenbeispiel:
   Datenbreite: 4 Bit
   Gegeben sei die Zahl 5. Diese soll in die Zahl -5 umgewandelt werden:
   Dezimal 5 → Binär 0101
   0101 bitweise invertieren → 1010
   Um 1 erhöhen: 1010 + 1 = 1011
   Somit: Dezimal -5 → Binär 1011
   
   Dezimaläquivalent einer binären vorzeichenbehafteten Zahl berechnen:
   A. Alle Bits haben die gleiche Wertigkeit wie bei der positiven Darstellung
   B. Die Wertigkeit des höchstwertigsten Bit's (MSB) ist negativ
   
   Zahlenbeispiel:
   Datenbreite: 4 Bit
   Gegeben sei die binäre Zahl 1011. Was ist der entsprechende Dezimalwert?
   Wertigkeit: -8 +4 +2 +1
   Binärzahl:   1  0  1  1
   Dezimal:    -8    +2 +1 = -5
   Somit: Binär 1011 → Dezimal -5

3.10 Rechnen mit binären Operatoren

Beim Low-Level-Programmieren von z.B. Mikrokontrollern (Arduino) und in der Kommunikation können Berechnungen auf binärer Ebene (HEX, BIN) Vorteile bringen, wie z.B. eine schellere Programmausführung. Darum soll hier kurz auf dieses Thema eingegangen werden.

x >> n bedeutet: Bitabfolge x um n-Stellen nach rechts verschieben (Rechts fallen die Bits heraus)
x << n bedeutet: Bitabfolge x um n-Stellen nach links verschieben (Neue 0-Bits werden rechts eingefügt)
& AND (UND WHT: 00=0 / 01=0 / 10=0 / 11=1)
| OR  (ODER WHT: 00=0 / 01=1 / 10=1 / 11=1)
^ XOR (Exklusives ODER WHT: 00=0 / 01=1 / 10=1 / 11=0)
~ NOT (Inverter z.B. 1011→0100)
(Die zur Verfügung stehende Bitbreite ist zu beachten! Data-Overflow)

Ganzzahlige Division durch 2
Zahlenbeispiel 1: 12 div 2 = 6
12 = 1100
1100 >> 1 = 110
110 = 6

Zahlenbeispiel 2: 15 div 2 = 7
15 = 1111
1111 >> 1 = 111
111 = 7

Restwert (Modulo) bei Division durch 2
LSB prüfen: 0→Rest-0, 1→Rest-1

Multiplikation mit dem Faktor 2
Zahlenbeispiel: 13 mul 2 = 26
13 = 1101
1101 << 1 = 11010
11010 = 26

Addition von 2 Bits inkl. Übertrag (Volladdierer)
(A=1.Bit, B=2.Bit, S=Summe, C1=Übertrag In, C2=Übertrag Out)
S = (A^B) ^ C1
C2= (A&B) | (C1&(A^B))

Zahlenbeispiel 1+0+1=10 oder 2
A = 1 (1. Bit)
B = 0 (2. Bit)
C1= 1 (Bit aus der vorangegangenen Binärstelle)
S = 0 (Summe)
C2= 1 (Übertrag in die nächste Binärstelle)

Bit auslesen
Zahlenbeispiel: Zweites Bit von links auslesen
a=0110
b=0011
c=0100
a & c = 0100
b & c = 0000

Bit setzen
Zahlenbeispiel: Zweites Bit von links setzen
a=0010
b=0110
c=0100
a | c = 0110 (Bit wurde gesetzt)
b | c = 0110 (Bit war schon gesetzt)

Bit löschen
Zahlenbeispiel: Zweites Bit von links löschen
a=0010
b=0110
c=0100   (Hinweis: ~c = 1011)
a & ~c = 0010 (Bit war schon gelöscht)
b & ~c = 0010 (Bit wurde gelöscht)

3.11 Gleitkommazahlen

Die Norm IEEE 754 definiert Standarddarstellungen für binäre Gleitkommazahlen in Computern in unter anderem den beiden Grunddatenformate 32 Bit → Single Precision und 64 Bit → Double Precision.
Eine Gleitkommazahl wird wie folgt dargestellt: x = v * m * b ^e
v: Vorzeichen → 1 Bit
m: Mantisse → Single:23Bit, Double:52Bit
b: Basis → Bei normalisierten Gleitkommazahlen ist b=2
e: Exponent → Single:8Bit, Double:11Bit

3.12 Byte-Reihenfolge Big/Little-Endian

Die Byte-Reihenfolge bezeichnet die Speicherorganisation für einfache Zahlenwerte (z.B. Integer) im Arbeitsspeicher.

• Big-endian-Format (Grossendig): Das höchstwertige Byte wird zuerst gespeichert, d. h. an der kleinsten Speicheradresse. Die höchstwertige Komponente wird zuerst genannt. Bsp. Uhrzeit → Stunde:Minute:Sekunde.
  Mikroprozessor: Das Motorola-Format steht für Big-Endian.
  Serielle Übertragung: Big-Endian-Byte-Reihenfolge → Das höchstwertige Bit eines Bytes wird zuerst übertragen. Bsp.: I²C
• Little-endian-Format (Kleinendig): Das kleinstwertige Byte wird an der Anfangsadresse gespeichert. Die kleinstwertige Komponente wird zuerst genannt. Bsp. Datum → Tag.Monat.Jahr.
  Mikroprozessor: Das Intel-Format steht für Little-Endian.
  Serielle Übertragung: Das niedrigstwertige Bit eines Bytes wird zuerst übertragen. Bsp.: RS-232

4. Datenübertragung und Speicherung

4.1 Das Taktsignal

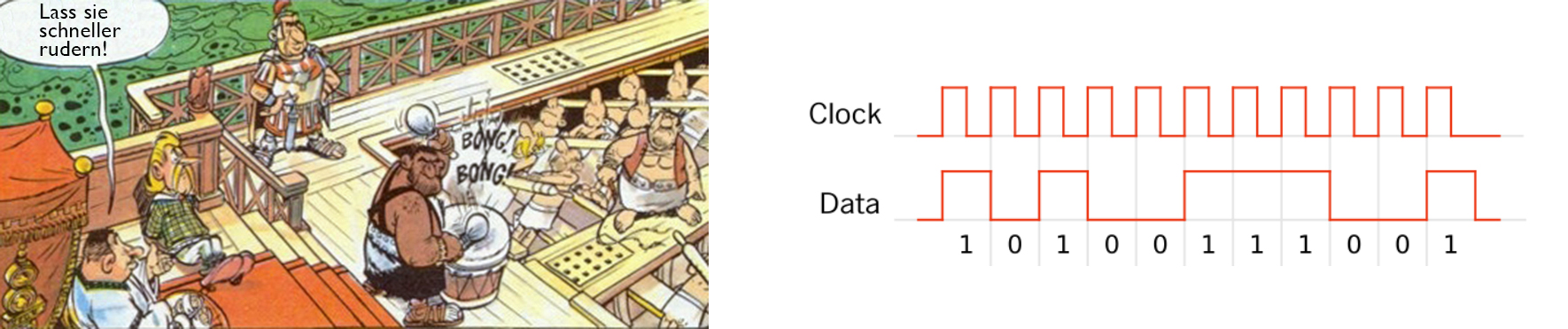
Die Benutzung eines Taktsignals (Takt, Clock Signalclock) ist ein Verfahren, den richtigen zeitlichen Ablauf beim Betrieb einer elektronischen Schaltung sicherzustellen. Insbesondere benötigen viele digitale Schaltungen ein entsprechendes Signal zur zeitlichen Koordination bzw. Synchronisation der Aktionen mehrerer Schaltkreise (insbesondere der von Flipflops bzw. Speicherzellen) innerhalb komplexer digitaler Systeme.
Das Taktsignal ist ein periodisches Signal, das durch seine Frequenz (Taktfrequenz, Taktrate) bzw. deren Kehrwert (Periodendauer) charakterisiert ist. Es wechselt dabei zwischen zwei Logikpegeln High (1) und Low (0) ab. Prominentes Beispiel eines Taktsignals ist der Systemtakt (System Clock) in einem Computer, der die Arbeitsgeschwindigkeit vieler Komponenten, insbesondere des Mikroprozessors, bestimmt.
Die Einheit der Taktfrequenz ist Hertz (Hz). Ein Hertz entspricht einem Takt pro Sekunde.

4.2 Parallele Datenübertragung

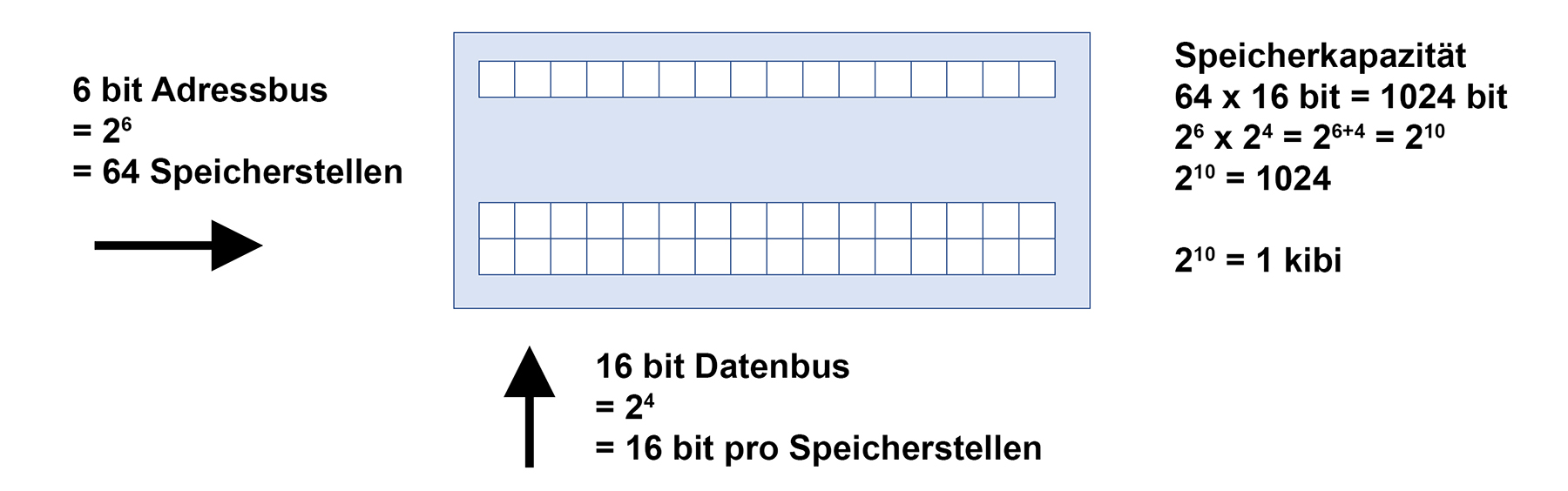
Eine parallele Verbindung zwischen zwei oder mehreren Komponenten nennt man Datenbus. Ein Codewort wird auf parallelen Leitungen auf einen Schlag bzw. Takt übertragen. Ist das Codewort z.B. 4 Bit breit, benötigt man 4 Leitungen.

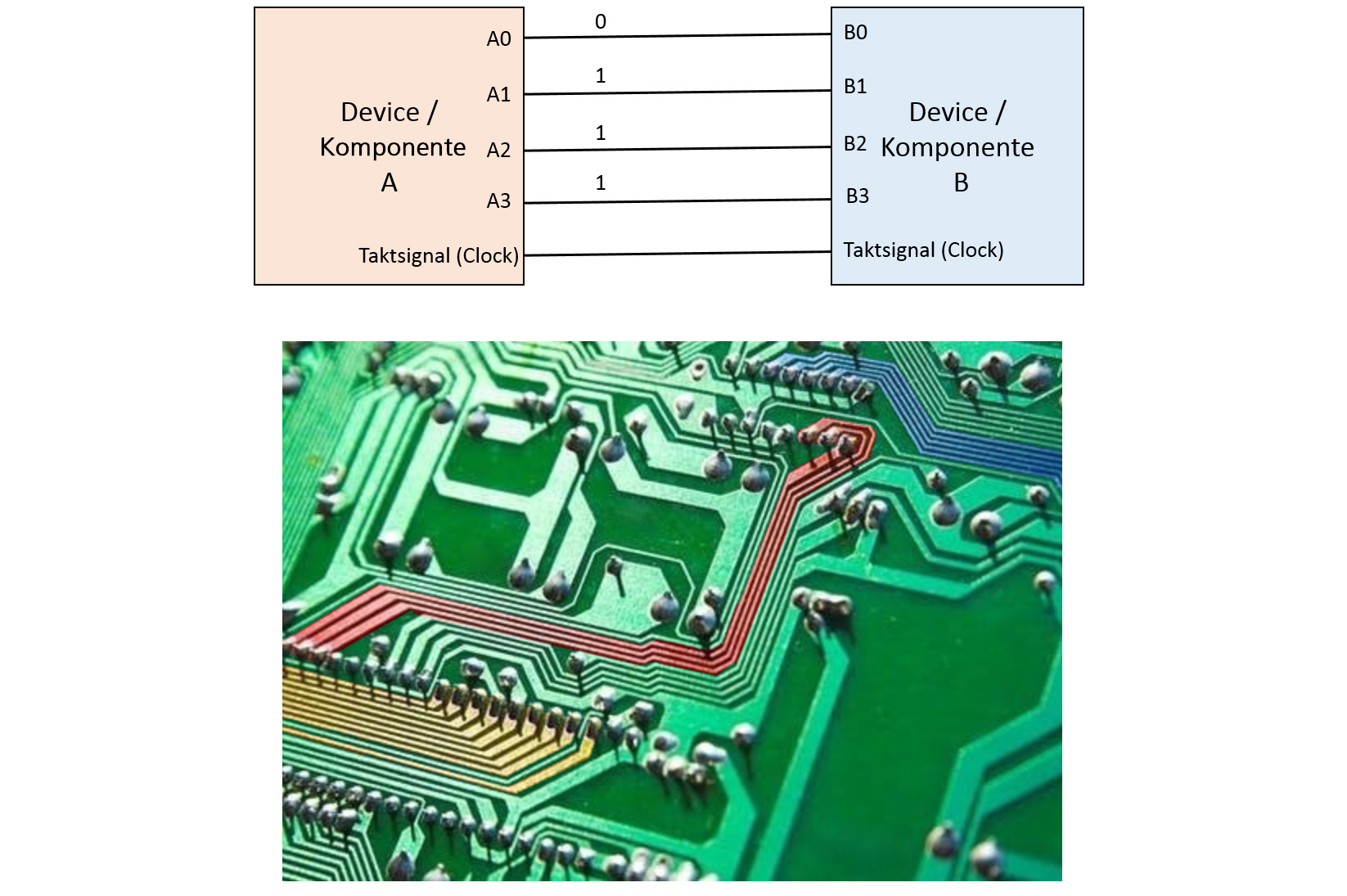
• Datenbus auf dem Mainboard: Verbindet CPU, RAM und I/O.
• Adressbus auf dem Mainboard: Verbindet CPU, RAM und I/O.
• SCSI (Small Computer System Interface): Verbindung und Datenübertragung zwischen Peripheriegeräten und Computern.
• P-ATA (Parallel Advanced Technology Attachment): Paralleler Datentransfer zwischen Speichermedien bzw. Laufwerken und der entsprechenden Schnittstelle eines Computers.
• Centronics-Schnittstelle für Drucker (Veraltet!)

4.3 Serielle Datenübertragung

Um Leitungen einzusparen, kann ein Codewort auch seriell übertragen werden. Dann werden die Bit's nacheinander "auf den Weg geschickt". Der Takt ist jeweils der Startschuss für das "Loslaufen" des folgende Bit. Um die selbe Performance wie bei der parallelen Datenübertragung zu erreichen, muss die Elektronik entsprechend schneller sein. Um zum Beispiel die gleiche Datenmenge einer 4-Bit-Parallelverbindung zu erreichen, muss die serielle Verbindung 4x schneller liefern.

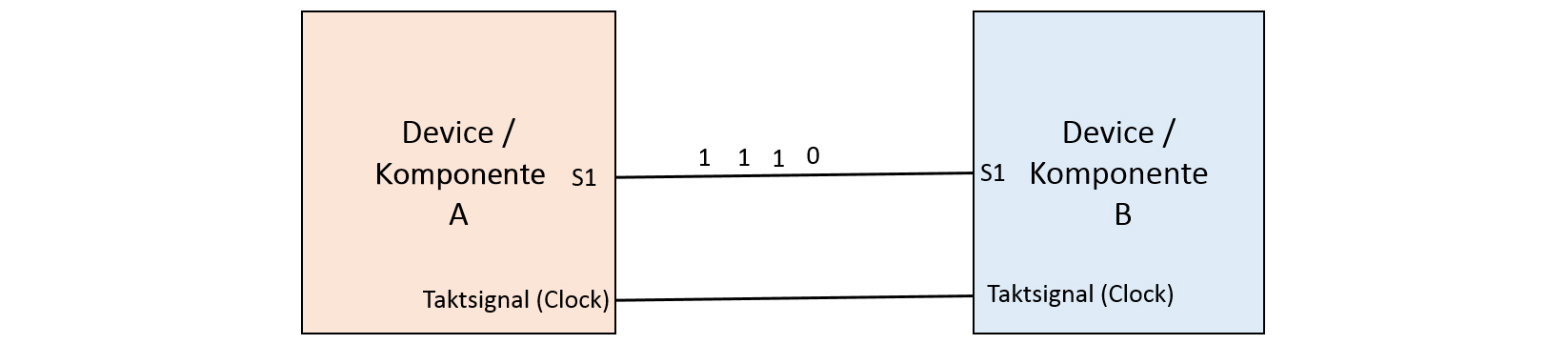
• S-ATA (Serial Advanced Technology Attachment): Serieller Datentransfer zwischen Speichermedien bzw. Laufwerken und der entsprechenden Schnittstelle eines Computers.
• USB (Universal Serial Bus) für Drucker, Speicher-Sticks etc.
• SAS (Serial Attached Small Computer System Interface): Die serielle Variante von SCSI.
• RS-232: Früher für Druckeranschluss. Heute teils noch in der verarbeitenden Industrie (Maschinen) zu finden.

Rechnungsbeispiele

• Datenübertragungsrate: Ein 8 Bit breiter Datenbus (Parallel) wird mit 1kHz getaktet. Wie gross ist die Datenübertragungsrate in kb/s und kB/s?
  Takt bedeutet: Pro Takt gehen in diesem Fall gleichzeitig 8 Bit über die Leitung
  Der Takt wird in Hz [Hertz] gemessen. Gemeint sind Anzahl Schwingungen (oder Takte) pro Sekunde. 
  1kHz → 1'000 mal "irgendwas" pro Sek.
  1kHz Takt bedeutet hier, dass pro Sekunde 1000 Mal 8 Bit über den Datenbus geschickt werden → Pro Sekunde 1'000 Takte zu je 8 Bit
  Somit in Bit und pro Sekunde: 1'000Hertz x 8Bit = 8'000Bit/sec oder 8kb/s.
  Oder eben in Byte und pro Sekunde: 1'000Hertz x 1Byte = 1'000 Byte/sec oder 1kB/s.
• Datenbusbreite: Ein paralleler Datenbus wird mit 1kHz getaktet. Es werden 8kb/sec übertragen. Wie breit ist der Datenbus?
  Das ist die Umkehrung der vorangegangenen Berechnung! 8000 / 1000 = 8. Also ist der Bus 8 Bit breit.

4.4 Datenspeicherung

Man unterscheidet zwei Arten von Speichertechnologien:

• Nichtflüchtiger oder permanenter Speicher: Dieser Speicher verliert seine Daten im stromlosen Zustand nicht.
  Typische Vertreter: Magnet-Harddisk, SSD, USB-Speicherstick.
  Man nennt solchen Speicher auch Sekundärspeicher.
• Flüchtiger Speicher: Dieser Speicher verliert seinen Inhalt, wenn er stromlos wird. Die Technologie solcher Speicher lässt wesentlich höhere Datenraten zu, als bei nichtflüchtigem Speicher.
  Typische Vertreter: Cache-Speicher in der CPU, RAM,
  Man nennt den RAM-Speicher auch Primärspeicher.
  Diese Speicher zeichnen sich darin aus, dass sie elektrisch bzw. verbindungstechnisch immer sehr nahe an der CPU liegen und von der CPU oft benötige Daten sehr schnell liefern bzw. zwischenspeichern können. (Effizienz, Performance)

Der Zugriff auf flüchtigen RAM-Speicher

Eine Analogie aus der Bücherwelt: Das Bücherarchiv.
Möchte man gerne seine archivierten Bücher wieder finden, muss man sich bei deren Ablage merken, wo man sie hinlegt. So ist es zum Beispiel sicher keine schlechte Idee, sich Regal- und Tablarnummer zu merken. Vielleicht sind die Bücher dann ja auch noch durchnummeriert. Gemeint ist selbstverständlich nicht die 12 bändige Micky-Maus-Best-Of-Sammlung sondern eine fast unüberschaubare Büchersammlung wie sie z.B. eine Universität besitzt.
Wir unterscheiden also Ware (Daten) und Ablageort (Adresse).
Beim Computer ist die Problemstellung dieselbe: Die erzeugten und gespeicherten Daten wollen wieder gefunden werden. Dafür verwendet man einen Speicher-Chip, mit vielen "Speichernischen". Jede "Speichernische" wird über eine eindeutige Adresse erreicht:

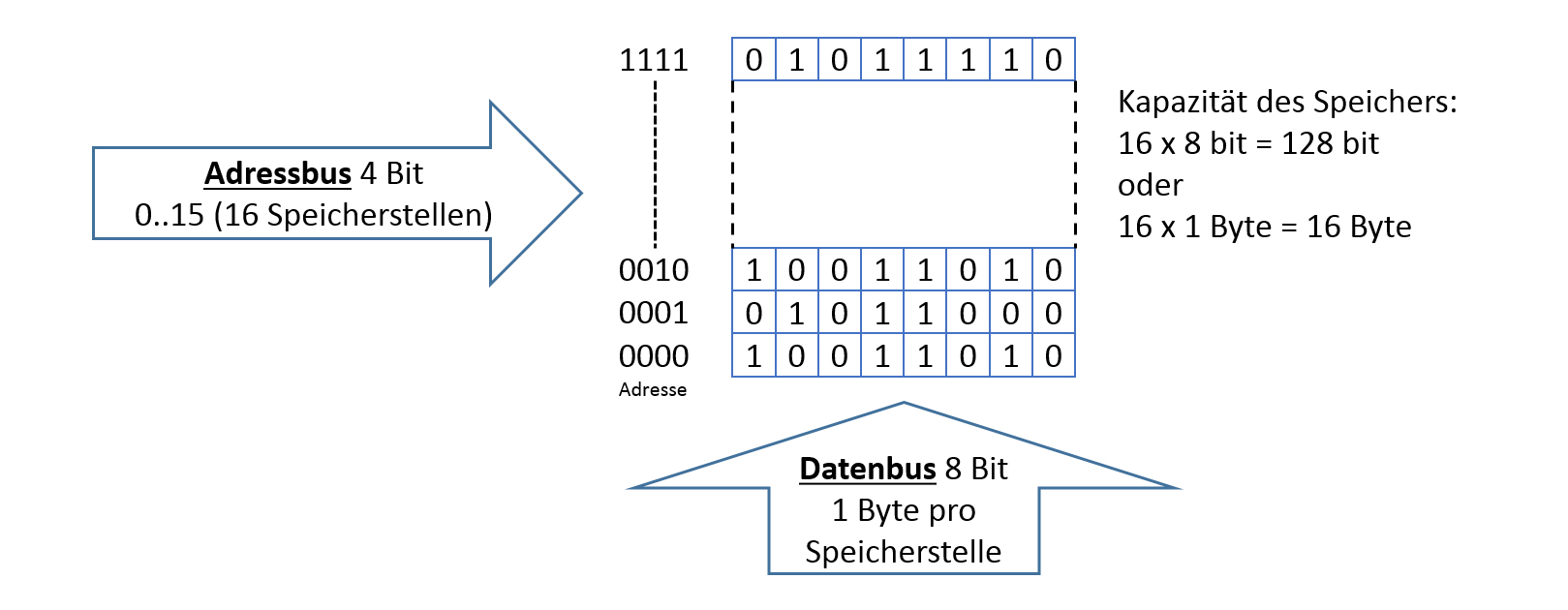
Bits und Bytes auf dem Speichermedium

Daten liegen in Form von Bits und Bytes auf einem Speichermedium. Solange sie noch in Bearbeitung sind, auf dem flüchtigen Primärspeicher (Memory, RAM), wenn sie danach dauerhaft abgelegt werden sollen, auf dem Sekundärspeicher (Harddisk, SSD) oder einem Backupmedium (CD, DVD, BluRyay, DAT, DLT, VLT etc.).
Beim Sekundärspeicher gibt das gewählte Dateisystem vor, wie die Daten auf dem Medium organisiert sind.
Zum Speichern von Daten nun ein paar Begriffserklärungen:

• Dateisystem: Ablageorganisation auf einem Datenträger. Dateien können gespeichert, gelesen, verändert oder gelöscht werden.
• FAT32: File Allocation Table → Dateisystem. (Dateien dürfen max. bis zu 4 GiB gross werden; Keine Berechtigungen/Zugriffsrechte)
• e3xFAT: Einer der verbesserten Nachfolger vom FAT32.
• NTFS: New Technology File System von Microsoft für Windows. Kleine Dateien und Verzeichnisse werden aus Effizienzgründen direkt in der MFT "Master File Table" abgespeichert. Flexible Rechteverwaltung durch Verwendung von ACL "Access Control List"
• Sektor: Kleinste verwaltbare Einheit auf dem Harddisk (512 Byte)
• Cluster (WIN) / Block (LIN): Logische Zusammenfassung von Sektoren auf einem Datenträger. Kleinste vom Betriebssystem verwaltbare Einheit. Die Clustergrösse lässt sich beim Formatieren einer Harddisk bestimmen, muss aber ein Vielfaches der Sektorgrösse sein. (WIN-typisch bzw. Default: 4kB)
• Partition: Unterteilung von Datenträgern. Jede Partition erhält unter WIN einen eigenen Laufwerksbuchstaben.
• MasterBootRecord: Der erste Datenblock eines partitionierten Speichermediums. Enthält Startprogramm (Bootloader)
• Formatierung: Vorbereitung eines Speichermediums zur Aufnahme von Daten.
• Kontingentierung: Den verwendbaren Festplattenplatz für einzelne Nutzer beschränken.

Rechnungsbeispiel

Speichergrösse: Ein Speicherbaustein wird durch einen 8 Bit breiten Datenbus versorgt. Zusätzlich führt ein 4 Bit breiter Adressbus an den Chip. Wieviele Bits fasst dieser Speicher? → Dazu stelle man sich eine Schlafzimmerkommode mit vielen Schubladen vor. In jeder Schublade haben 8 Bit Platz. Will man nun Datenbits in einer Schublade speichern, sollte man sich merken, in welche Schublade man diese Bits versorgt. Dazu dient die Adresse. Da es sich hier um eine 4 Bit Adresse handelt, ergeben sich 2*2*2*2=16 Speicher-"Schubladen". Die Schubladen bzw. der Speicher kann also maximal 16 * 8 Bit Speichern. Das wären dann 128 Bit.

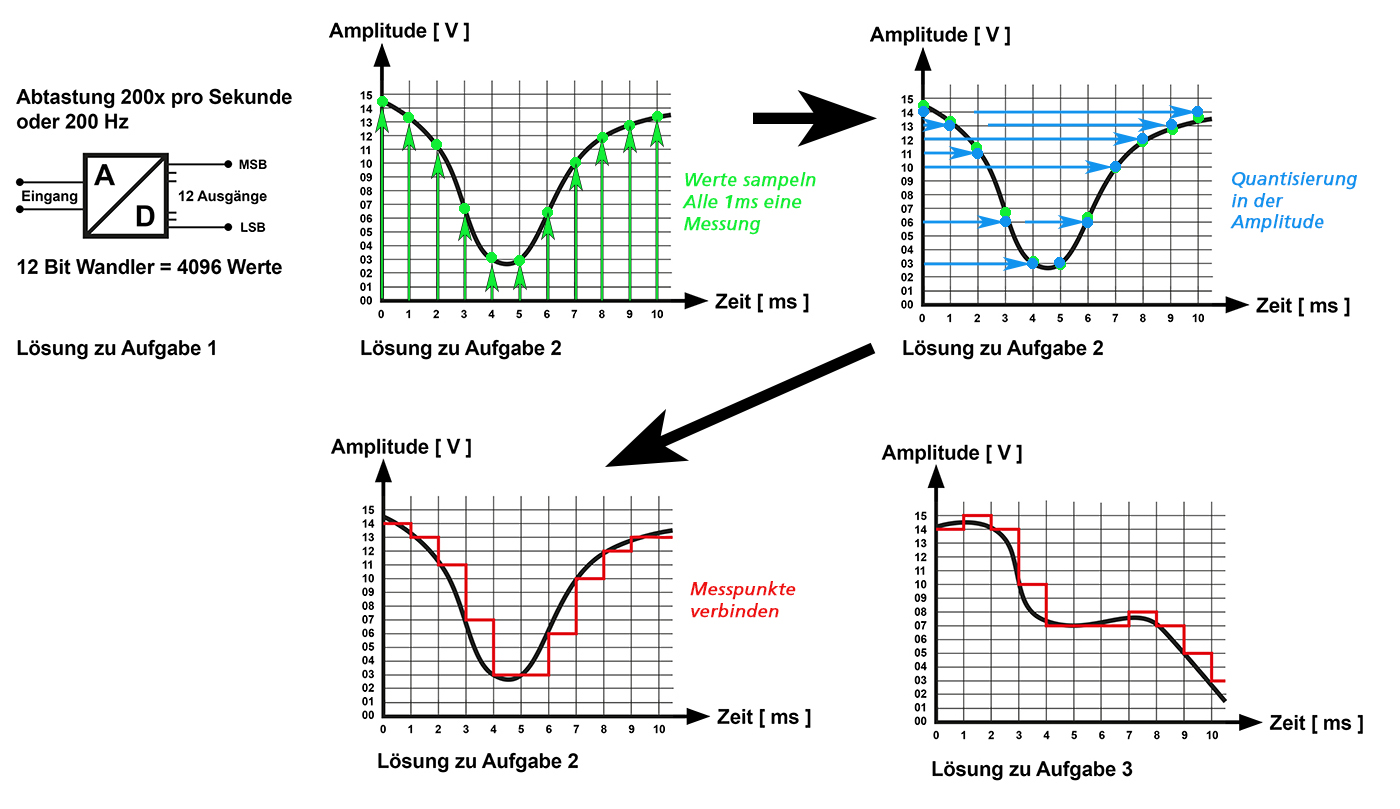
5. Analog-Digital-Wandlung

Die ALU (Aritmetische Logische Einheit) im Mikroprozessor verarbeitet nur Daten in binärer Form. Somit müssen von Sensoren zugeführte analoge Werte zuerst digitalisiert werden. Dazu dienen A/D-Wandler. Gewisse Mikrokontroller haben A/D-Wandler bereits im Chip "miteingepackt".
Da die ALU Resultate auch wieder in binärer Form ausgibt, müssen diese für periphere Geräte wie Aktoren wieder in die analoge Form gewandelt werden. Dazu dienen D/A-Wandler. Auch solche sind bei einigen Mikrokontrollern bereits an Bord.
Im folgenden wird nur die A/D-Wandlung behandelt!

Und so funktioniert es:

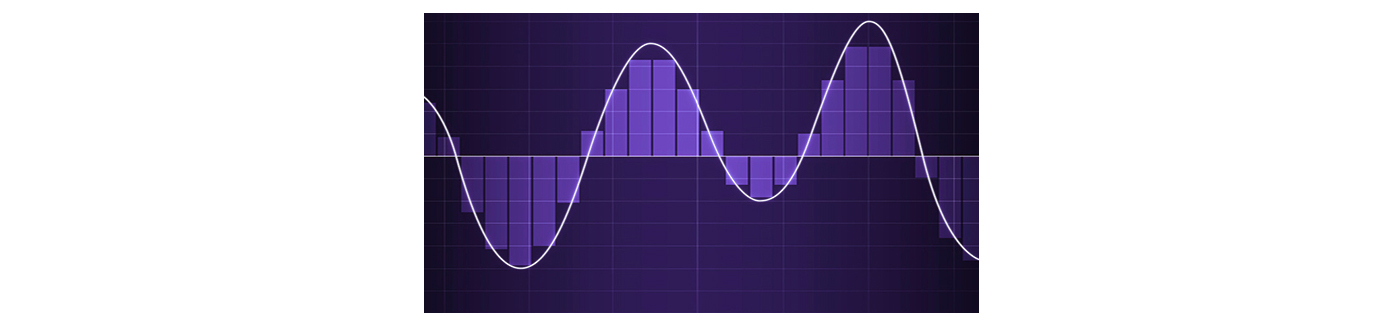
Ein digitale Signal kann aus einem Analogsignal, welches den zeitlich kontinuierlichen Verlauf einer physikalischen Grösse beschreibt, durch die Quantisierung und eine Abtastung/Sampling, welche zu definierten Zeitpunkten erfolgt, gebildet werden. Die digitalen Werte sind üblicherweise als Binärzahlen/Dualcode kodiert, so dass ihre Quantisierung in Bits angegeben wird. Analog-Digitalwandlung eines Audiosignals: 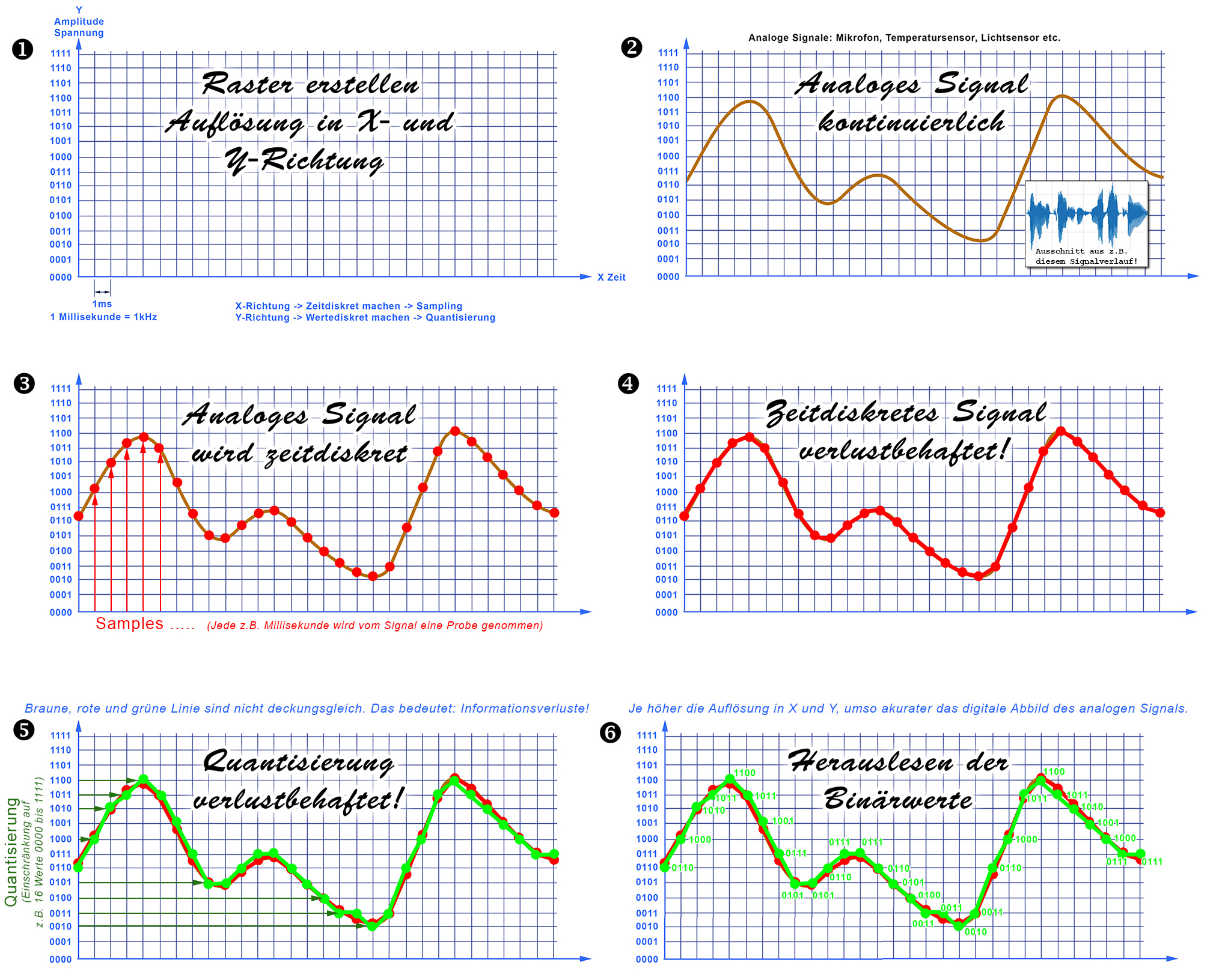Die Digitalisierung eines analogen Signals hat immer zur Folge, dass das originale analoge Signal nicht mehr verlustlos rekonstruiert werden kann. Je nach Abtastrate und Auflösung kann man aber das digitale Signal in ein qualitativ befriedigendes analoges Signal zurückverwandeln. Der von der Digitalisierung herführende Treppeneffekt bzw. die dadurch entstehenden Oberwellen beim zurückverwandelten Analogsignal können mit entsprechenden analogen Filtern (Tiefpassfilter) unterdrückt bzw. herausgefiltert werden.

Rechnungsbeispiel

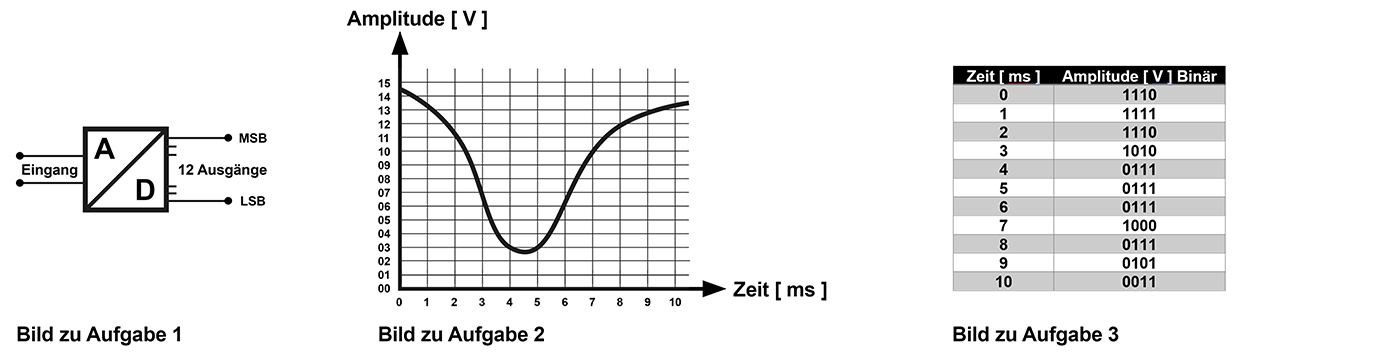
Analog-Digital-Wandler: Ein A/D-Wandler hat 4 Ausgänge. Er misst das Analogsignal 100x pro Sekunde oder anders ausgerückt: Die Samplingrate beträgt 100 Hertz. Wie viele Bit werden pro Sekunde gespeichert?
4 Ausgänge am A/D-Wandler bedeutet 4 Bit pro Messung (oder 2*2*2*2=16 unterscheidbare analoge Eingangswerte, was aber in dieser Aufgabe nicht gefragt war). Da pro Sekunde 100x gemessen wird, ergeben sich pro Sekunde 100 x 3 = 400 Bit, also 400Bit/sec.