Codesysteme

1. Einführung

Dieser Kurs soll aufzeigen, wie binäre Daten durch Abmachungen (Codes) zu interpretieren sind, damit daraus Informationen werden.
Dem Begriff «CODE» begegnet man in vielen Bereichen, darum soll zuerst eine Auslegeordnung erstellt werden, wo überall von «CODEs» gesprochen wird:

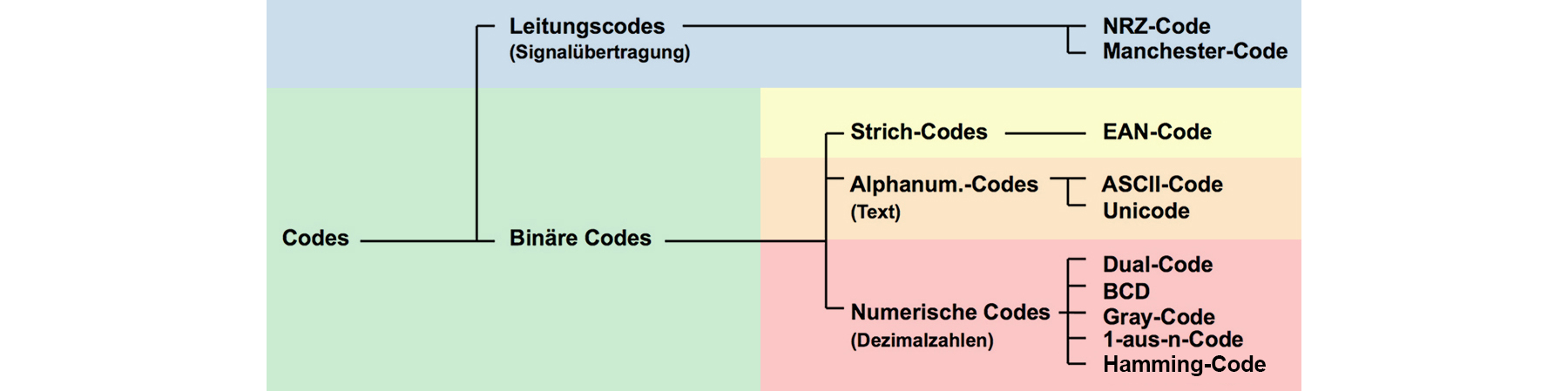
• Numerische Codes
  Werden im Computer verwendet, um ganze Zahlen in binären Zeichen darzustellen (Binärcodes) wie z.B. Dualcode, BCD, Graycode, Aikencode, Exzess-3-Code, 1-aus-n-Code und weitere
• Alphanumerische Codes
  Z.B. ASCII-Code oder Unicode und wird im Computer verwendet, um Buchstaben, Zahlen und Satzzeichen durch Bitfolgen darzustellen
• Strich-Code
  Z.B. der EAN-Code auf Verpackungen
• Leitungscodes
  Bei der Datenübertragung werden die sog. Leitungscodes so aufgebaut, dass sie sich möglichst optimal an die Eigenschaften des Übertragungsmediums anpassen wie Unterdrückung eines Gleichspannungsanteils, Taktrückgewinnung etc. Beispiele: Manchester-Code bei Ethernet, NRZ-Code, Eight-to-Fourteen-Modulation (EFM) bei CD's, 8B10B-Code (Gigabit Ethernet) etc.
• Media-Codecs
  CoDec → CodierungDecodierung → MP3-Code, MPEG2-Code, MPEG-4-AVC-Code, Reed-Solomon-Code (Audio-CD)
• Maschinen-Code
  Wird in der Computertechnik verwendet. Stellt ein Programm bzw. eine Art
  Vorgehensbeschreibung für den Prozessor dar
• Quellcode
  Beim Programmieren kodiert man Algorithmen als Quellcode in einer
  Programmiersprache wie zB. C++, Java, etc. den man übrigens später in
  Maschinencode übersetzt bzw. kompiliert oder HTML-Code der von einem
  Webbrowser interpretiert wird (Negativbeispiel Spaghetti-Code ;-)
• Geheimcode
  Mit monoalphabetischer Verschlüsselung werden Buchstaben durch
  andere Buchstaben ersetzt (Verschlüsselungsverfahren)
• ISBN-Code
  International Standard Book Number zur Identifizierung von Büchern
• Genetischer Code
  Eine biologische Anleitung, nach der während der Proteinbiosynthese die
  Informationen der DNA/RNA in Aminosäuresequenzen übersetzt werden

Hier behandelte Codes

Codes nicht verwechseln, mit...

• Protokoll wie z.B.
  • Internet Protokoll → Grundlegendes Netzwerkprotokoll des Internets
  • Netzwerkprotokoll → Kommunikationsprotokoll im Netzwerkumfeld
  • Kommunikationsprotokoll → Regelwerk zum Datenaustausch
  • Sicherheitsprotokoll → Authentifikation von Subjekten, Absicherung bzw. Nachweis von Daten bzw. Kommunikation vor Veränderung bzw. Auslesung
  • Transaktionsprotokoll → bei Datenbanken
• Datenformat → ist ein Begriff aus der Datenverarbeitung, der festlegt, wie Daten strukturiert und dargestellt werden und wie sie bei ihrer Verarbeitung zu interpretieren sind. Dateiformate werden in der Regel durch Software-Hersteller oder durch ein standardisierendes Gremium festgelegt. In einer Spezifikation sollte die Art der Codierung und Anordnung von Daten innerhalb eines Dateiformats genau beschrieben werden.

1.1 Begriffsdefinition «CODE»

Unter «Code» versteht man die eindeutige Abbildung der Zeichen eines ersten Zeichenvorrats-1 auf die Zeichen eines zweiten Zeichenvorrats

Beispiel: Erster Zeichenvorrat:  0,1
          Zweiter Zeichenvorrat: ♦, ♥, ♣, ♠
          Code (Tabelle)         00 → ♦
                                 01 → ♥
                                 10 → ♣
                                 11 → ♠

• Vorschrift, wie Nachrichten oder Befehle zur Übertragung oder Weiterverarbeitung für ein Zielsystem umgewandelt werden. Beispielsweise stellt der Morsecode eine Beziehung zwischen Buchstaben und einer Abfolge kurzer und langer Tonsignale her
• Der Code heisst entzifferbar, wenn es eine eindeutige Umkehrabbildung gibt, die jedem Nachrichtenwort aus B wieder das ursprüngliche Wort aus A zuordnet

1.2 Eigenschaften von Codes

Verschiedenartige Anwendungen erfordern verschieden spezialisierte Codes. Zum Beispiel kann eine ökonomische Darstellung der Codewörter verlangt sein um Übertragungsgeschwindigkeit und Speicherplatzbedarf zu optimieren. Oder aber es soll eine Sicherung gegen Verfälschung implementiert sein, um Übertragungsfehler oder Verarbeitungsfehler einzuschränken oder gar zu verhindern. Auch der Schutz vor unbefugtem Zugriff ist denkbar, wo man mit Verschlüsselungstechnik die Geheimhaltung gewährleisten will.

Die folgenden Spezialisierungen bzw. Codemerkmale beschränken sich auf binäre Codes (Dualcodes):

• Stellenzahl/Zeichenvorrat (2ˆStellenanzahl = Anzahl mögliche Zeichen)
• Redundanz (Redundanz=Stellenzahl-Logarithmus zur Basis 2 / Anzahl realisierter Zeichen)
• Gewichtung der einzelnen Binärstellen (zB. beim Dualcode wäre dies 1-2-4-8)
• Erkennen/korrigieren von Übertragungsfehlern (CRC, ECC, Hammingdistanz)
• Änderung nur einer Binärstelle beim Übergang zum nächsten Zahlenwert (Einschrittige Codes zB. Graycode)
• Minimierung der 0- oder 1-Bits (Verlustlose Kompression: Morsecode, VLC)
• Vereinfachte Komplementbildung (Bringt Vorteile bei der Berechnung von arithmetischen Ausdrücken, Signed Integer)
• Unterscheidung von Zahlen grösser/kleiner 5 (Für eine einfache arithmetische Zahlenrundung)
• Unterscheidung gerader/ungerader Zahlen (Vorteilhaft in der Arithmetik)

2. Numerische Codes

2.1 Binärcode

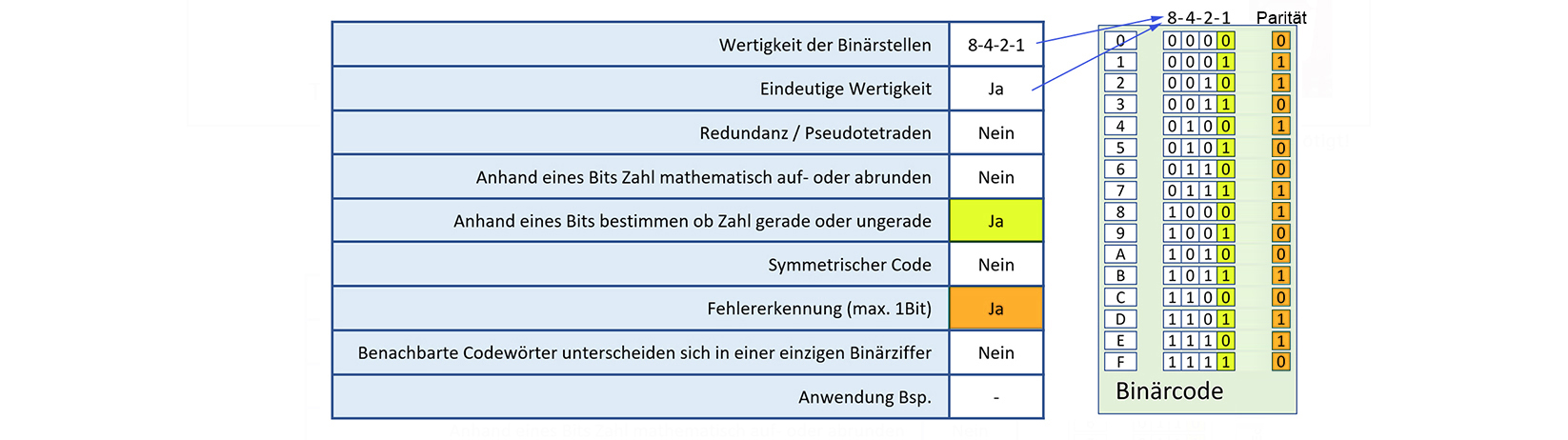
Der Binärcode ist der einfachste numerische Code. Es werden beim 4-Bit-Binärcode alle 16 Bitkombinatinen verwendet.

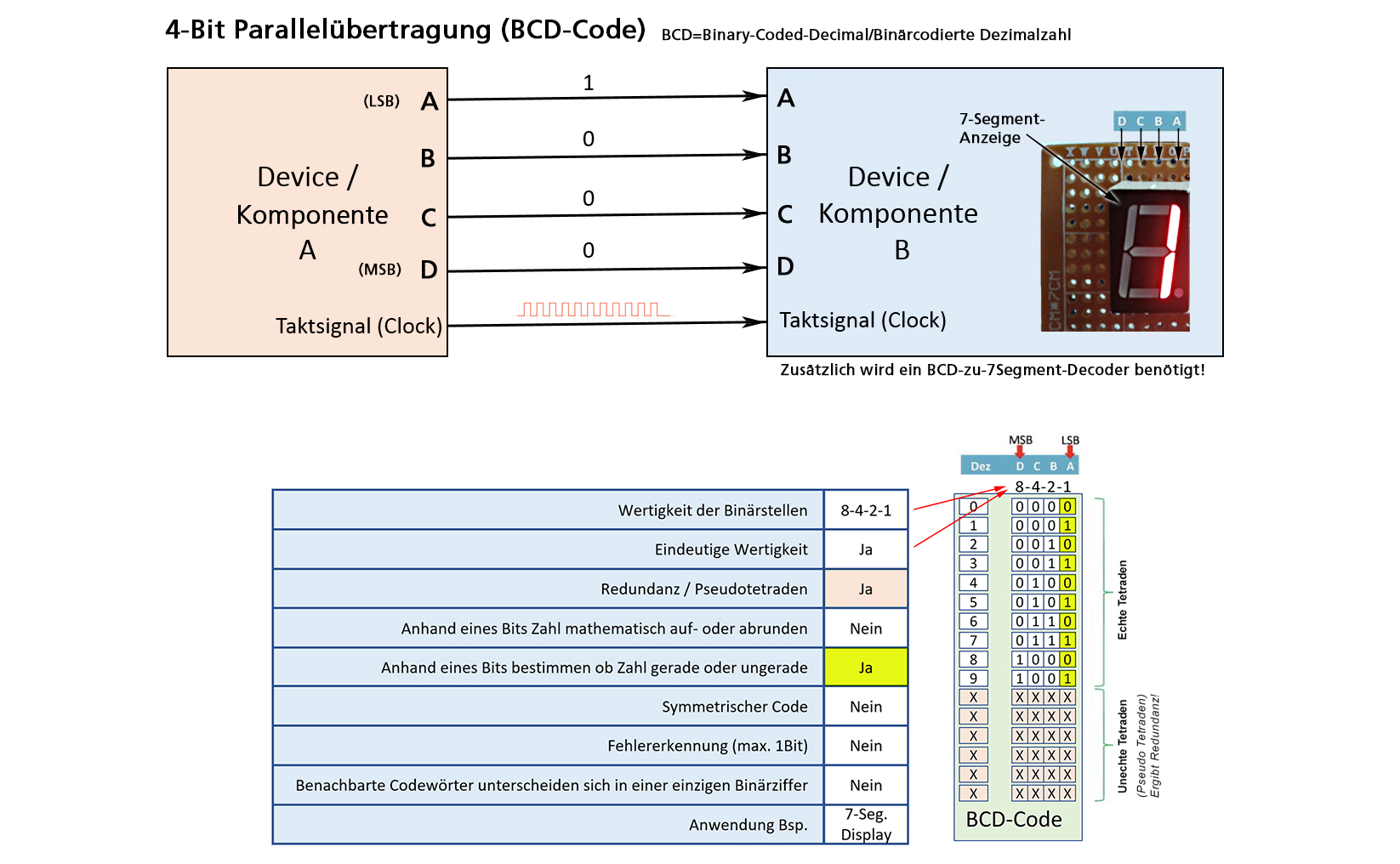
2.2 BCD (Binary Coded Decimal)

Das folgende Bild zeigt die Übertragung von einer einzigen Dezimalzahl im BCD-Code. Der BCD-Code ist ein simpler Binärcode, der nur die ersten zehn Bitkombinationen 0..9 nutzt und somit Redundanz aufweist. Die Wertigkeit ist wie beim Binärcode 8-4-2-1 und mit dem LSB kann ebenfalls festgestellt werden, ob die Zahl gerade oder ungerade ist. Die Codetabelle bildet die Basis für die Übertragung. Bemerkung: Heute werden für die Verbindung von elektronischen Komponenten (von und zu Mikrokontrollern) eher die Busse SPI (Serial Peripheral Interface) oder I²C (Inter-Integrated Circuit) verwendet.

2.3 Aiken-Code

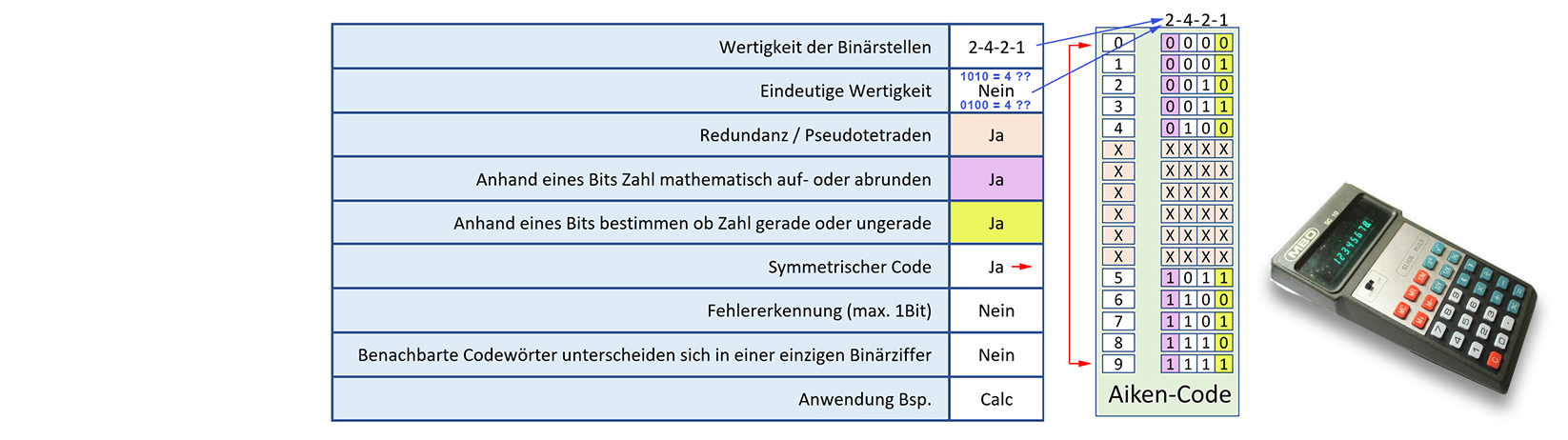
Der Aiken-Code ist für Taschenrechner optimiert. Vier Bit stellen, ähnlich dem BCD-Code, jeweils eine Dezimalzahl dar. Der Aiken-Code ist eindeutig definiert, obwohl seine 2-4-2-1-Wertigkeit mehrere Lösungen zulassen würde. Der Aiken-Code ist nämlich symmetrisch, was soviel bedeutet, dass nur die ersten fünf und letzten fünf Kombinationen genutzt werden. Daraus ergeben sich sechs Bitkombinationen, die nicht verwendet werden, sogenannte Pseudotetraden und somit Redundanz. Der Vorteil des Aiken-Codes liegt in der Anordnung der einzelnen Bits: Das MSB kann zur Rundung von Zahlen benutzt werden, das LSB zum feststellen, ob eine Zahl gerade oder ungerade ist. Die Symmetrie des Aiken-Codes läst eine schnelle Umwandung von positivem zu negativem Wert zu. Stichwort Komplementbildung. Dies wiederum ein Vorteil beim z.B. Subtrahieren. Aus «7-3» wird «7+(-3)»

2.4 «2-aus-5»-Code

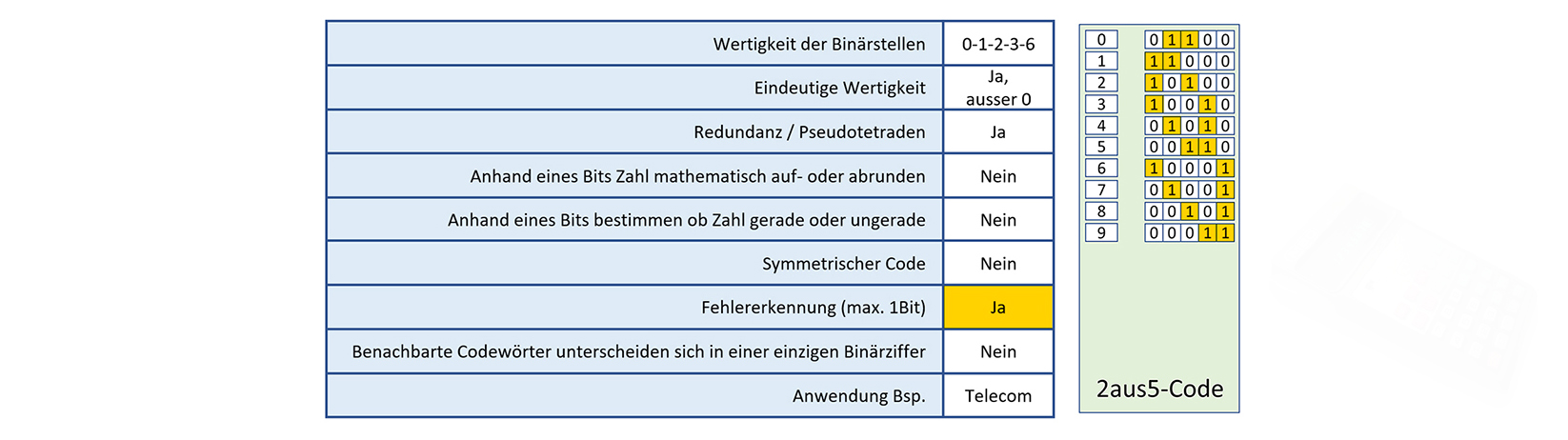
2-aus-5-Code bedeutet: Jeweils 2 Bit sind binär «1», die restlichen drei Bit sind binär «0». Es sind pro Dezimalwert nur immer zwei Bit's auf logisch "1". Somit kann mit einer Quersumme (=2) eine fehlerhafte Bitübertragung festgestellt werden. Allerdings auch nicht ganz zuverlässig. Sollten sich z.B. ein 0-Bit und ein 1-Bit "gedreht" haben, merkt man das später selbstverständlich nicht, weil die Summe ja immer noch 2 ist. Hier bieten Hamming-Codes mehr Sicherheit.

2.5 «1-aus-n»-Code

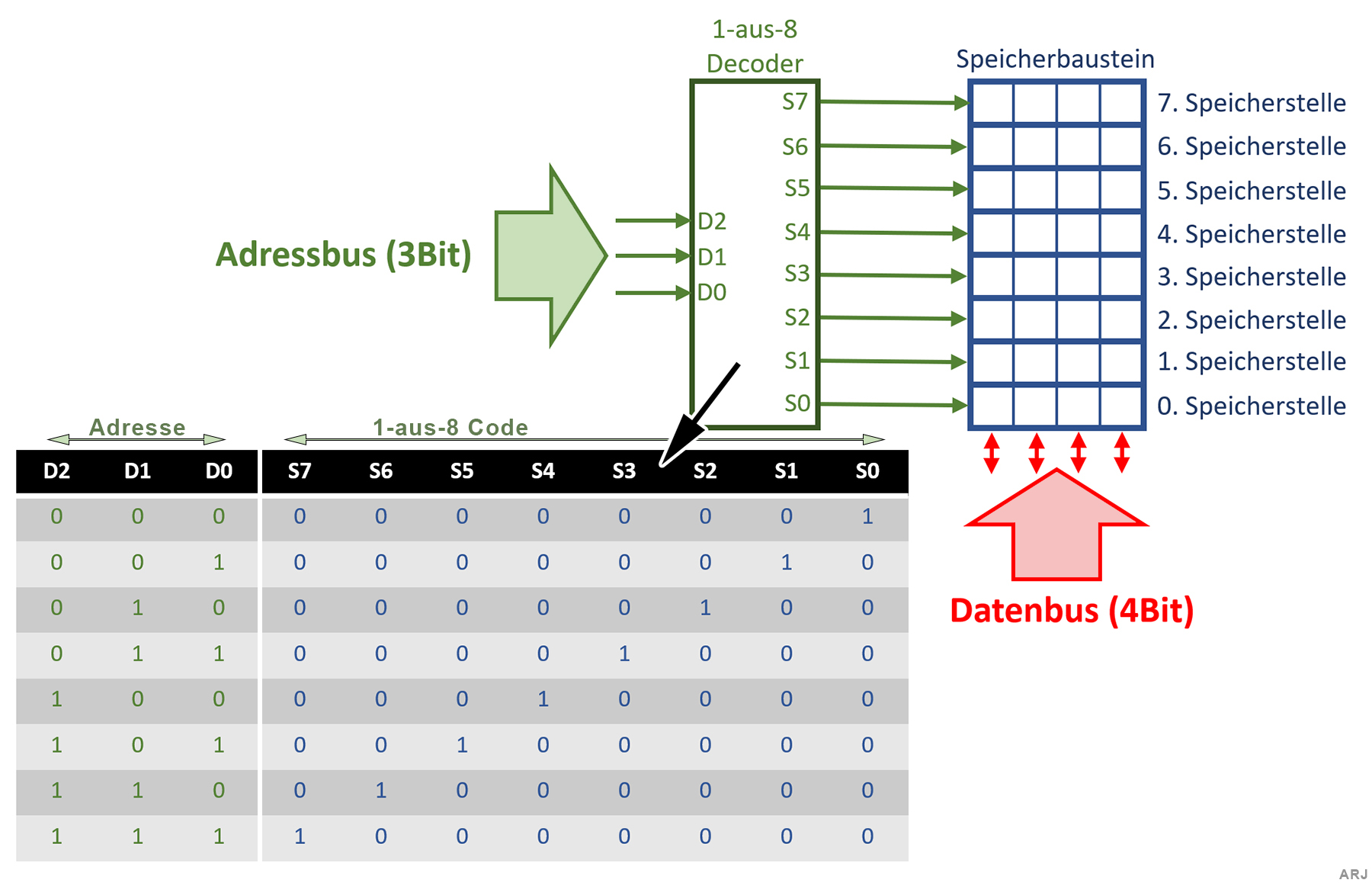
1-aus-n Codes trifft man in Speicherchips, Tastaturen (Matrix), Displays (Matrix) etc. an. Im folgenden der vereinfachte Aufbau eines 32-Bit Speicherchips:

2.6 Graycode

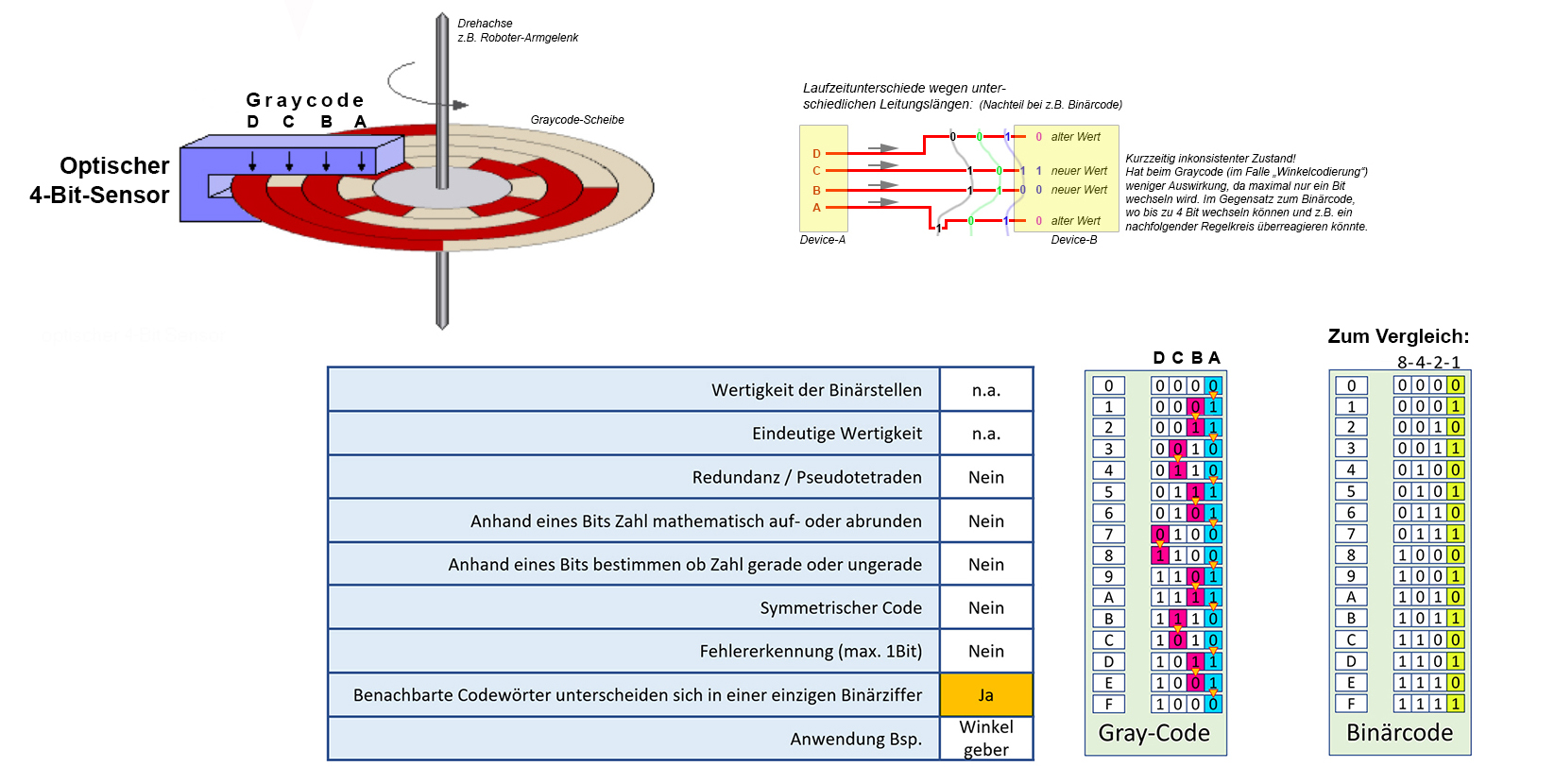
Der Vorteil dieses Codes liegt darin, dass sich benachbarte Codewörter nur in einer einzigen binären Ziffer unterscheiden und dabei Übertragungsfehler verringert werden können, weil bei kontinuierlich ändernden digitalen Signalen auf mehradrigen Leitungen sich unterschiedliche Laufzeiten nicht auswirken können.
Dieser Code ist z.B. für die Erfassung eines Drehwinkels geeignet. Der Graycode lässt sich wie folgt aus dem Binärcode ableiten:

1. Zahl1 = Binärcode der gewünschten Zahl
2. Zahl2 = Rechtsshift der Zahl1 um 1 Bit
3. Graycode = Zahl1 XOR Zahl2

2.7 Binärcode mit Fehlererkennung (Parität)

Mit einem Paritätsbit lässt sich feststellen, ob während der Datenübertragung ein Bit gewechselt hat. Das Paritätsbit einer Folge von Bits dient als Ergänzungsbit, um die Anzahl der mit 1 belegten Bits (inklusive Paritätsbit) der Folge auf z.B. Gerade (Even) zu ergänzen. Im Gegensatz zum nachfolgenden Hammingcode kann mit dem Paritätscheck ein fehlerhaftes Bit erkannt aber nicht lokalisiert werden. Allerdings ist Vorsicht geboten: Zwei falsch übertragene Bits würden beim Empfänger nach Überprüfung durch das Paritätsbit den falschen Eindruck erwecken, dass die Übermittlung erfolgreich war.

2.8 Der Hammingcode (ECC)

Der Hammingcode ist ein selbstkorrigierender Code (ECC → Error Correcting Code, Fehlerkorrektur). Die Besonderheit dieses Codes besteht in der Verwendung mehrerer Paritätsbits. Diese Bits ergänzen jeweils unterschiedlich gewählte Gruppen von den die Information tragenden Nutzdatenbits. Durch eine geschickte Wahl der Gruppierung, deren mathematische Grundlagen im Folgenden an einem Beisoiel aufgezeigt wird, ist nicht nur eine Fehlererkennung, sondern auch eine Fehlerkorrektur der übertragenen Datenbits möglich.

Die einzelnen Codewörter des Hamming-Codes weisen einen Hamming-Abstand von 3 auf. Durch diesen Unterschied von jeweils drei Bitstellen kann der Decoder einen oder zwei Bitfehler in einem Datenblock erkennen, aber nur einen Bitfehler korrigieren. Bei zwei Bitfehlern liefert der Decoder ein gültiges, aber falsches Codewort.

Was bedeutet: Hamming-Abstand von 3? Dazu ein Beispiel:
  Zahl-A = 00101
  Zahl-B = 01110
Der Hamming-Abstand zwischen Zahl-A und Zahl-B ist 3 → Es müssen drei Bits geändert werden, um aus Zahl-A die Zahl-B zu erhalten

Hamming-Code → Beispiel

1. Wert kodieren und an Empfänger übertragen:
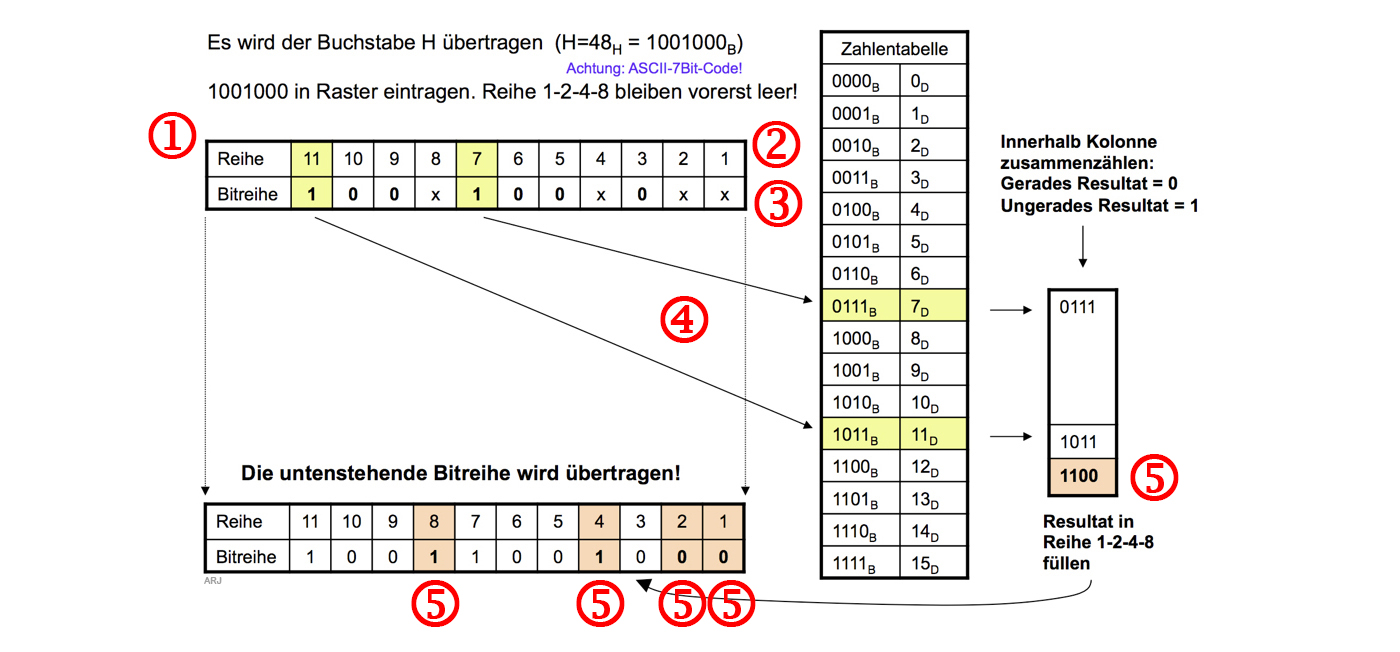
   • Tabelle mit 2x11 Zellen erstellen. [1]
   • Zellen mit 1..11 durchnummerieren. [2]
   • Die sieben Nutzdatenbits (Buchstaben "H" → 1001000) eintragen. Dabei die Zellen 1,2,4 und 8 auslassen. [3]
   • Die Position der Zellen 1..11, in der eine "1" steht [4], übertragslos addieren. [5]
   • Die erhaltenen 4 Bit dort in die Tabelle eintragen, wo die 4 Lücken bestehen. [5]
   
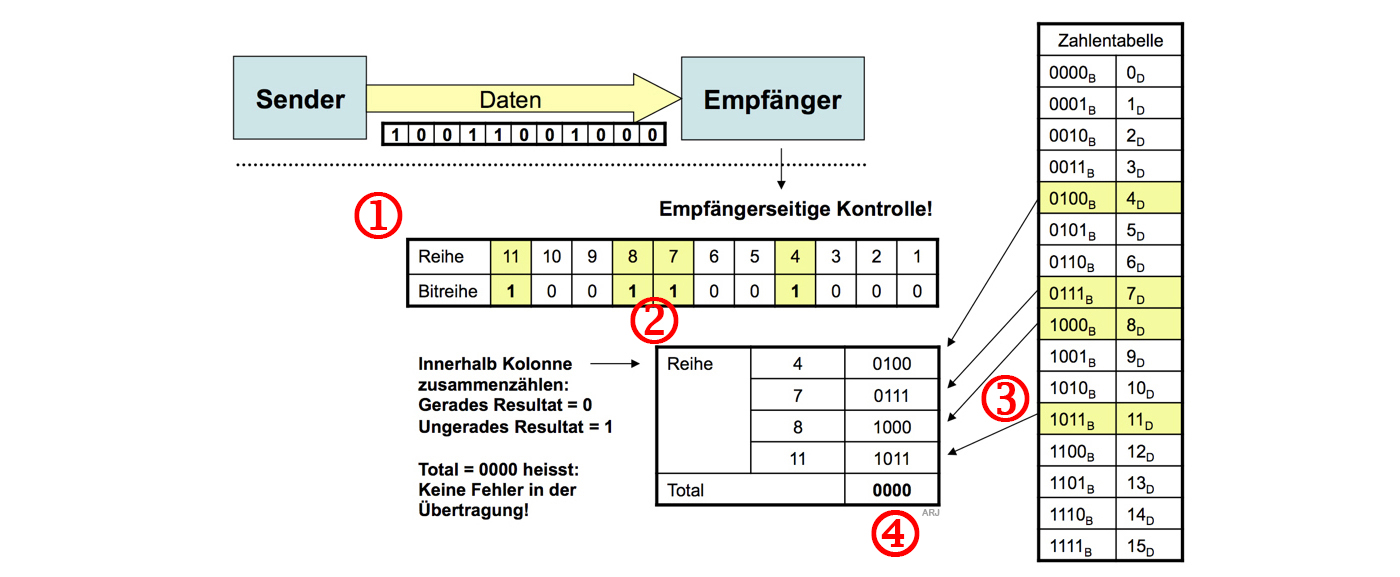
2. Fehlerloser Hamming-Code empfangen und auswerten:
   • Es wurden 11 Bit empfangen. Wiederum eine Tabelle mit 2x11 Zellen erstellen. [1]
   • Die Position der Zellen 1..11, in der eine "1" steht [2], übertragslos addieren. [3]
   • Wenn als Resultat 0000 entsteht, wurde kein Übertragungsfehler festgestellt. [4]
   
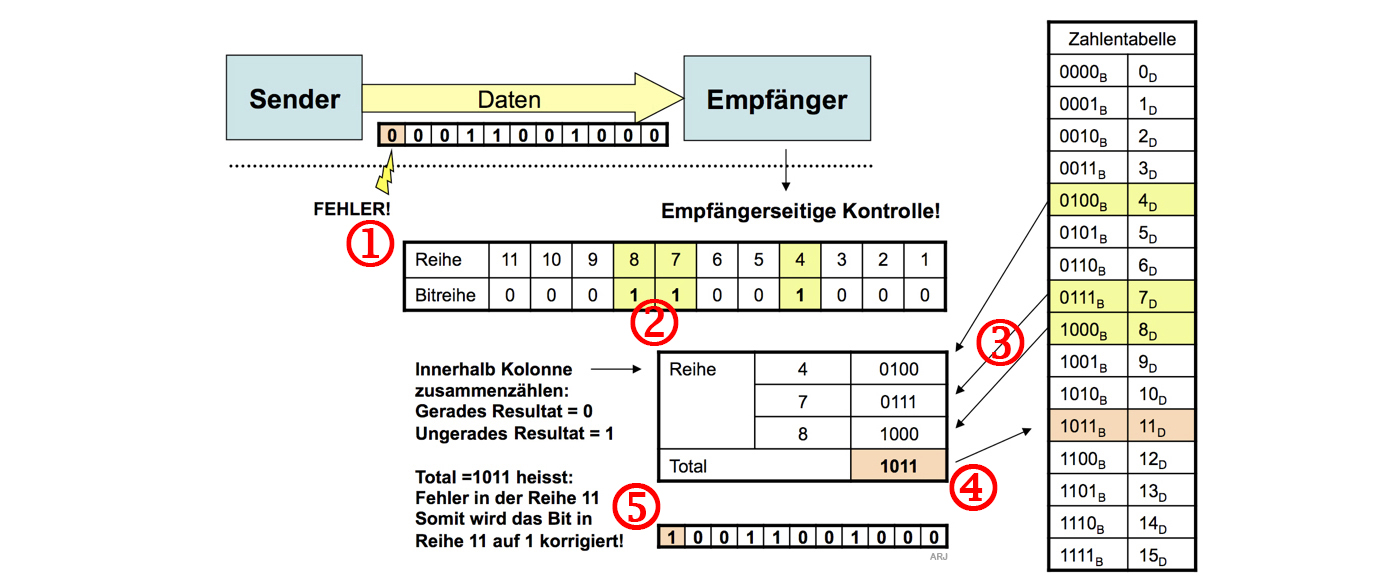
3. Durch Übertragungsfehler beschädigter Hamming-Code empfangen und auswerten:
   • Es wurden 11 Bit empfangen. Wiederum eine Tabelle mit 2x11 Zellen erstellen. [1]
   • Die Position der Zellen 1..11, in der eine "1" steht [2] übertragslos addieren. [3]
   • Als Resultat erhält man nicht 0000 sondern diesmal 1011. [4]
   • Diese 1011 deutet auf die fehlerhafte Stelle (1011=11) hin. Man kann nun das Bit "umkehren und die Nachricht ist somit "korrigiert". [5]
   

3. Leitungscodes

Bisher sind wir immer davon ausgegangen, dass neben der Datenleitung (Parallel oder Seriell) immer auch eine Verbindung mit dem Taktsignal bestehen muss. Auf Mainboards mag das ja gut sein. Bei Datenübertragungen über längere Distanzen ist eine Extra-Leitung für den Takt doch eher Materialverschwendung. Es musste also eine Lösung her. Man fand diese in einer ausgeklügelten Codierung, die den Takt bereits integriert hat und eine weitere Leitung somit erspart bleibt.
Im folgenden werden zwei typische Vetreter aus verschiedenen Anwendugsgebieten vorgestellt: Der Manchestercode für Ethernet und die Eight-to-Fourteen-Modulation (EFM) bei Music-CDs.

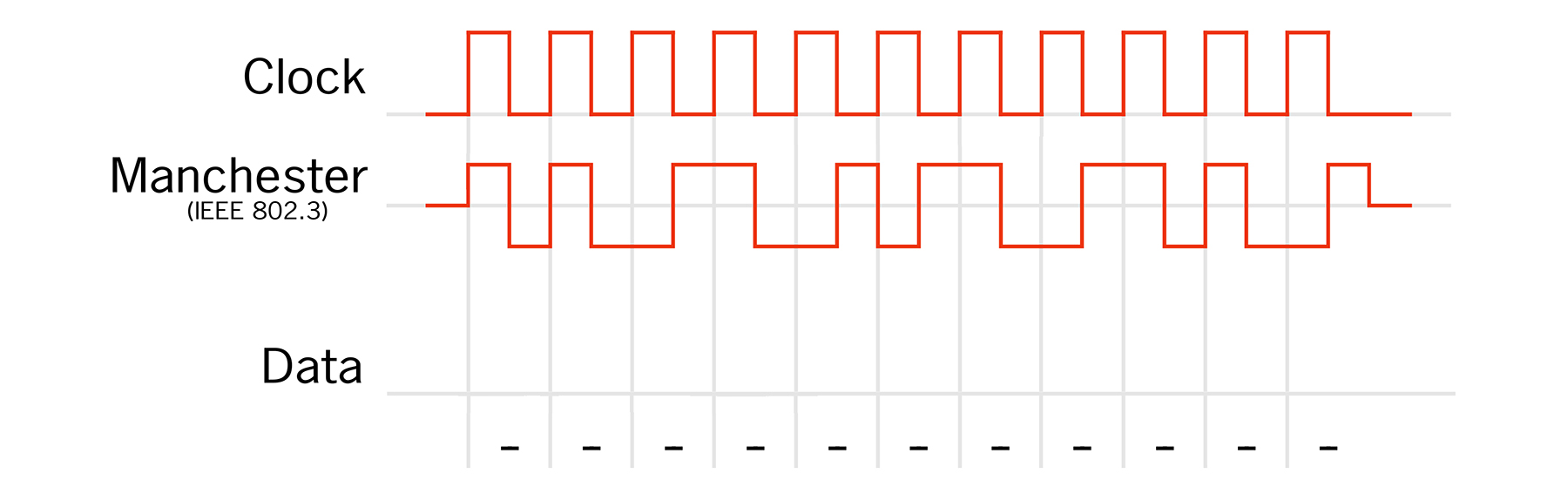
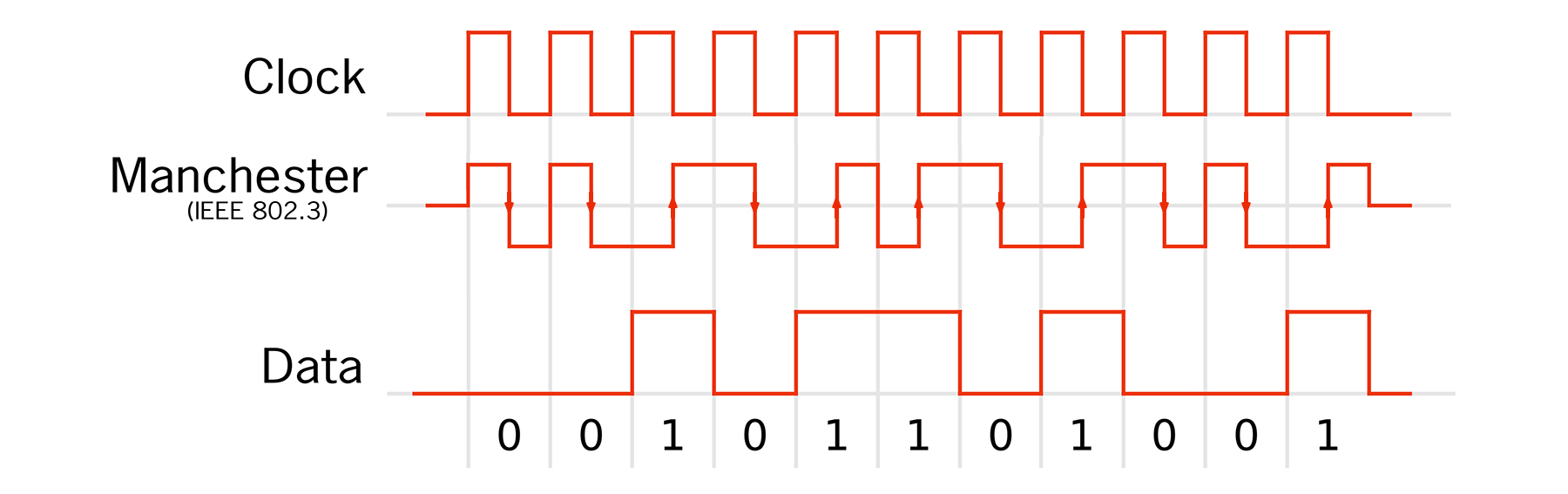
3.1 Der Manchestercode

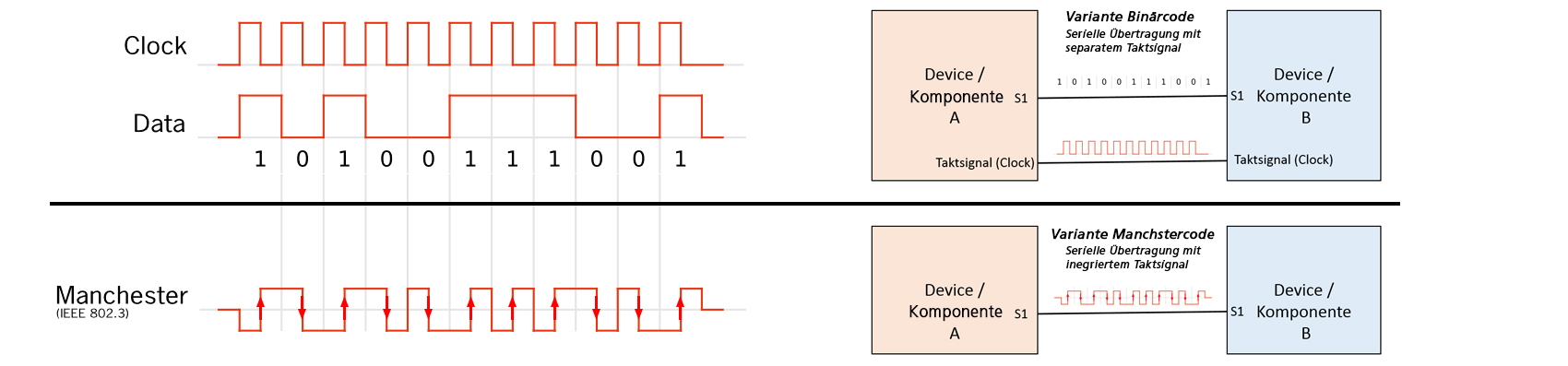
Der Manchester-Code ist ein Leitungscode, der bei der Kodierung das Taktsignal erhält. Die Flanken des Signals tragen bezogen auf das Taktsignal die Information. In der Codedefinition nach IEEE 802.3, wie sie bei 10-Mbit/s-Ethernet verwendet wird, bedeutet eine fallende Flanke eine logische Null und eine steigende Flanke eine logische Eins. In jedem Fall gibt es mindestens eine Flanke pro Bit, aus der das Taktsignal abgeleitet werden kann. Ein Nachteil der Manchester-Codierung ist, dass bei der Datenübertragung die benötigte Bandbreite doppelt so hoch ist wie bei der einfachen Binärcodierung.

3.2 Die Eight-to-Fourteen-Modulation (EFM) bei Music-CDs

EFM wird hauptsächlich bei der Datenaufzeichnung auf optischen Datenträgern wie Compact Discs (CDs) verwendet:
Das Abtasten einer CD erfolgt mittels einer Laserdiode. Der Laserstrahl wird an der CD reflektiert und eine Fotodioden registrieren Schwankungen in der Helligkeit. Die Umdrehungsgeschwindigkeit der Disk variert. Somit bleibt die Bahngeschwindigkeit am Lesekopf konstant.
Zur Aufzeichnung der Musikdaten auf die Music-CD müssen diese mit einer passenden Kanalkodierung (genauer: Leitungskodierung) kodiert werden. Dabei kommt EFM zur Anwendung.

EFM bedeutet: Jedem Byte wird ein 14 Bit langes Codewort aus einer standardisierten Tabelle zugeordnet. Zwischen diesen 14-Bit-Codewörtern werden drei Trennbits eingefügt. Für CD-Audio wird die Tabelle im Red Book festgelegt.

Auf einer Audio-CD sind die Daten in einer Spur in Form von Vertiefungen (Pits) und dazwischenliegenden Spurabschnitten ohne Vertiefungen (Lands) gespeichert. Ein kurzer Spurabschnitt von ca. 1/3 Mikrometer Länge (eine Bitzelle) entspricht einem Bit. Eine Eins repräsentiert einem Übergang von Pit zu Land oder von Land zu Pit, Nullen repräsentieren keinen Übergang (NRZ-M-Codierung). Um sicherzustellen, dass auch im Übergangsgebiet zwischen zwei 14-Bit-Codewörtern der Mindestabstand von 2 und der Höchstabstand von 10 Nullen (d.h. mindestens 3 und höchstens 11 Bit-Zellenlängen zwischen zwei Übergängen) gewahrt bleibt, werden zwischen den Codewörtern zusätzlich 3 Trennbits eingefügt.
Damit sich Kratzer und Produktionsfehler nicht negativ auf die Lesbarkeit der CD auswirken, sind die Daten mittels Reed-Solomon-Fehlerkorrektur gesichert, so dass Bitfehler erkannt und korrigiert werden können. 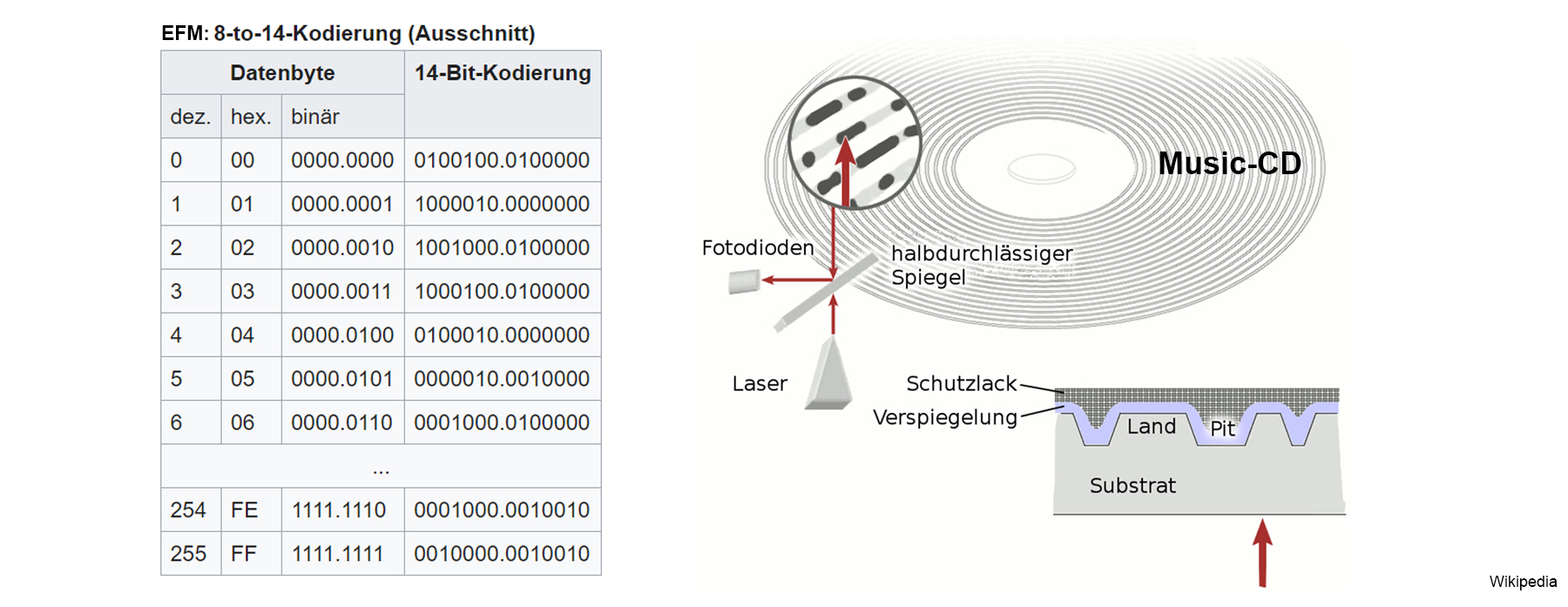Warum das datenintensive EFM? Schliesslich bläht EFM ein Byte auf 14 Bit auf und es kommen sogar noch drei Füllbits hinzu, was eine hohe Redundanz bedeutet: → Mit EFM wird den Eigenheiten des Speichermediums (optischen Abtastung, Form und Grösse der Pits) Rechnung getragen. Die EFM stellt sicher, dass sich alle drei bis elf Bitdauern die Polarität des ausgelesenen Signals ändert, dass also nach einer 1 zwei bis zehn 0 folgen. Das geschieht, wenn der Laser in der Spur einen Übergang von einer Vertiefung (Pit) zu einem Abschnitt ohne Vertiefung (Land) passiert oder umgekehrt. Weiterhin wird durch diese Kodierung eine wesentlich einfachere Signalverarbeitung erreicht, da dass Signal der Fotodioden keinen Gleichstromanteil enthält der entstünde, wenn man anstatt z.B. sieben "kurzen" 0 eine "lange" 0 auslesen würde. Die Abschnitte mit/ohne Vertiefungen müssen allerdings lang genug sein, damit der Laser die Veränderung erkennen kann. Würde man ein Bitmuster direkt auf den Datenträger schreiben, würden bei einem alternierenden Signal (10101010…) falsche Werte ausgelesen, da der Laser den Übergang von 1 nach 0 beziehungsweise von 0 nach 1 nicht verlässlich auslesen, ja sogar diese Übergänge gar nicht erst in der notwendigen Präzision in Kunststoff gepresst werden könnten.

4. Barcodes

Als Barcode oder Strichcode wird eine optoelektronisch lesbare Schrift bezeichnet, die aus verschieden breiten, parallelen Strichen und Lücken besteht. Der Begriff Code steht hierbei für Abbildung von Daten in binären Symbolen. Die Daten in einem Strichcode werden mit optischen Lesegeräten, wie z. B. Barcodelesegeräten (Scanner) oder Kameras, maschinell eingelesen und elektronisch weiterverarbeitet.

4.1 EAN-Code (European Article Number)

Das Bildchen mit den verschiedenbreiten schwarzen und weissen Balken, wie man es heutzutags auf allen Food- und Non-Food-Artikeln antrifft, repräsentiert eine 8-stellige (EAN-8) oder eine 13-stellige Zahl (EAN-13). Diese 8 oder 13 Zahlen sind vom Produkte-Hersteller oder einer Organisation weiter aufgeschlüsselt wie z.B. in Ländercode, Produktcode, Lotnummer, Datum, Prüfziffer etc. Im folgenden betrachten wir den EAN-8-Barcode, der 8 Dezimalzahlen repräsentiert, wovon die letzte eine Prüfziffer ist. Der EAN-13 ist sinngemäss gleich aufgebaut.

EAN-8

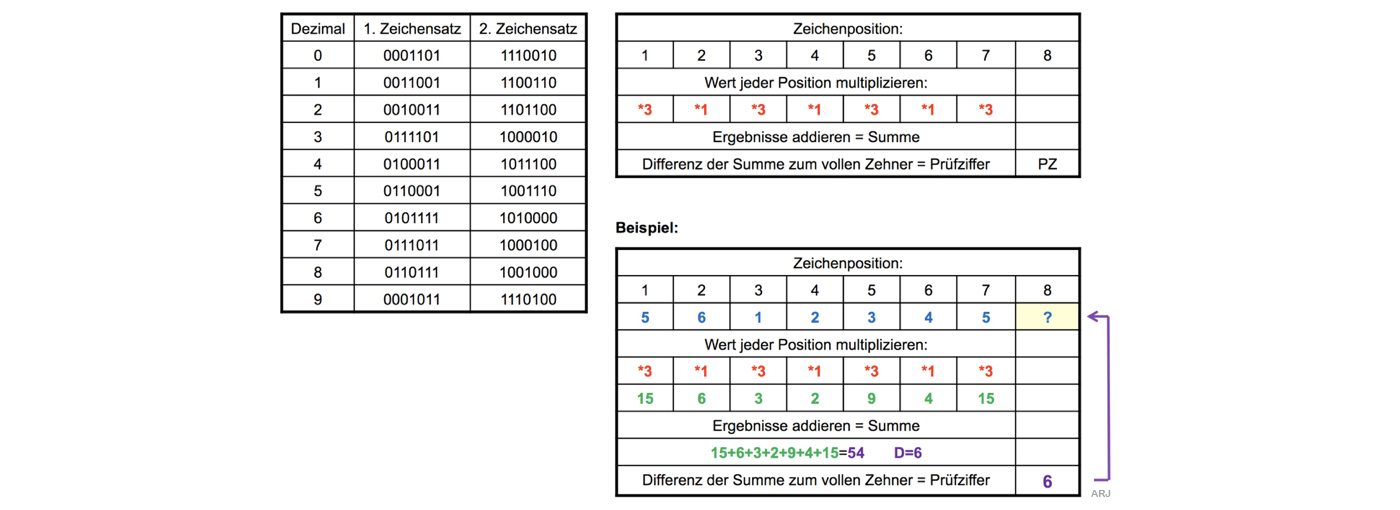
Der EAN-8-Barcode setzt sich vermeintlich aus dicken und dünnen Strichen zusammen. Optisch richtig aber technisch leider falsch. Beim EAN-Barcode besteht jedes Zeichen aus 7 gleich grossen Spalten. Je nach Codierung werden diese Spalten gefüllt oder leer gelassen, wobei gilt: 0=Leer 1=Gefüllt 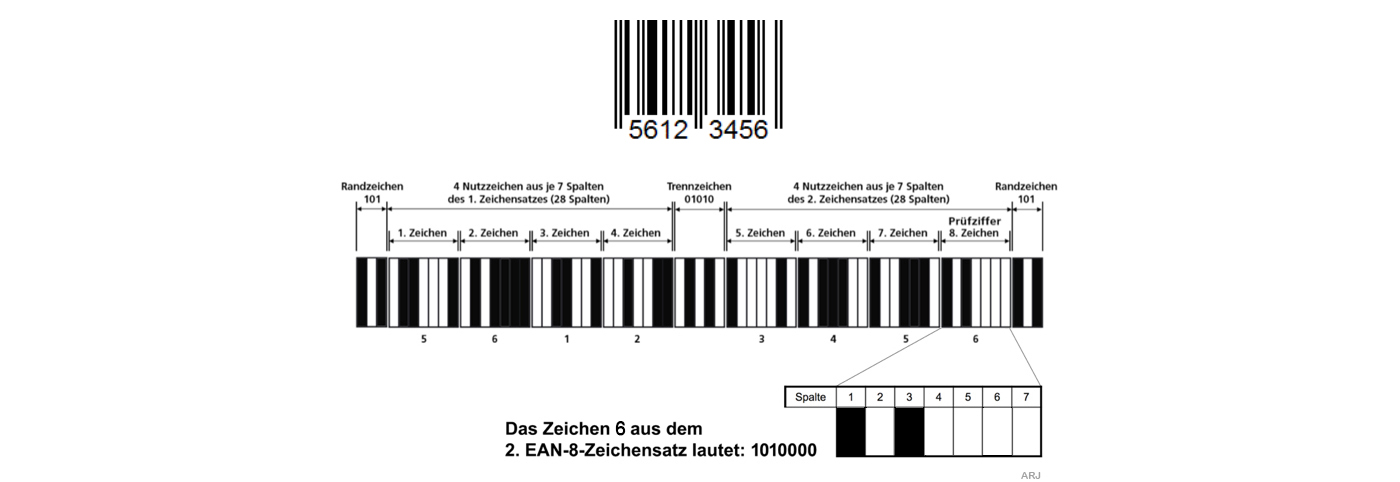Zum EAN-8-Code gehören auch Zeichensätze + Prüfziffer. Der erste wird für die vier linken «Balken» der zweite für die vier rechten «Balken» verwendet.

4.2 QR-Code (Quick Response)

Fehlerkorrektur-Levels zu) können bis zu 30% der QR-Grafik beschädigt oder verschmutzt sein, ohne die Lesbarkeit zu beinträchtigen (Fehlerkorrektur-Level "H"). Diese Eigenschaft wird oft zur Plazierung von Werbebildchen und Logos "missbraucht". Der maximale Informationsgehalt (177×177 Elemente, max. Verlust von 7% der Daten bzw. Fehlerkorrektur-Level "L") beträgt knapp 3kB. Das würde dann ca. 7000 Dezimalziffern oder 4300 alphanumerische Zeichen ergeben. Vorsicht: Weil der Inhalt eines QR-Codes nicht auf den ersten Blick ersichtlich ist, kann man einem Fake-Link auf schädliche Webseiten aufsitzen oder das Smartphon führt Malware aus.

5. Alphanumerische Codes

Alphaumerische Codes dienen der Darstellung von Text. Dazu gehören die Buchstaben A..Z, a..z, Satzzeichen wie zum Beispiel ?, !, :, die Zeichen für Nummern 0..9, aber auch semigraphische Zeichen wie Rechtecke, Dreiecke, Kreisflächen etc.

5.1 Der ASCII-Code

Der ASCII-Code (American Standard Code for Information Interchange) ist in seiner Ursprungsversion eine 7-Bit-Zeichenkodierung und wurde bereits damals eingesetzt, wo noch Textnachrichten per Fernschreiber (Telex) übermittelt wurden. Die druckbaren Zeichen umfassen das lateinische Alphabet in Gross- und Kleinschreibung, die zehn arabischen Ziffern sowie einige Interpunktionszeichen (Satzzeichen, Wortzeichen) und andere Sonderzeichen. Der Zeichenvorrat entspricht weitgehend dem einer Tastatur oder Schreibmaschine für die englische Sprache. Die nicht druckbaren Steuerzeichen enthalten Ausgabezeichen wie Zeilenvorschub oder Tabulator, Protokollzeichen wie Übertragungsende oder Bestätigung und Trennzeichen wie Datensatztrennzeichen.

Die 7-Bit ASCII-Tabelle mit den Binär-, Dezimal- und Hexadezimalwerten der 128 Characters (Gelb: Steuerzeichen)

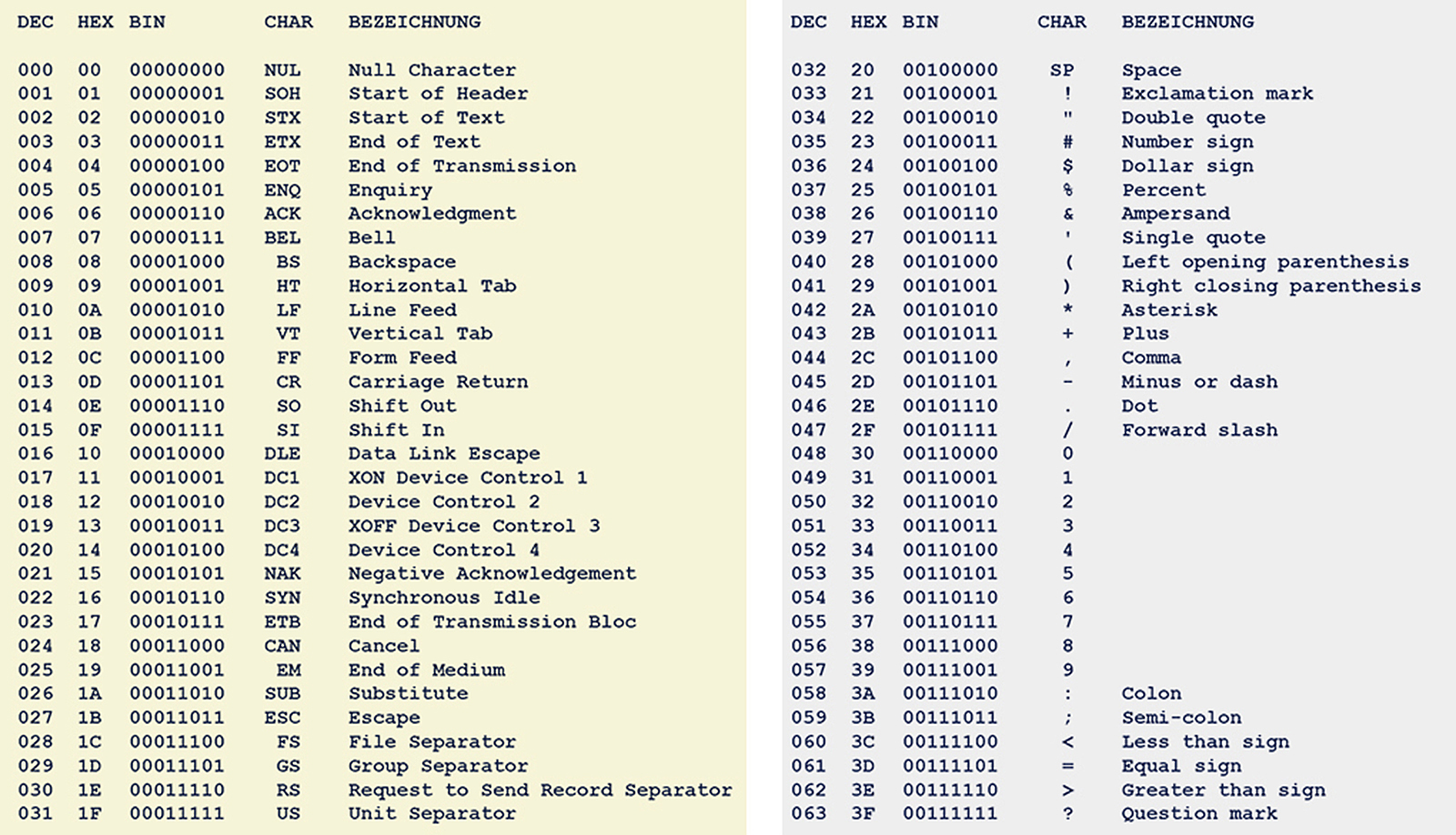
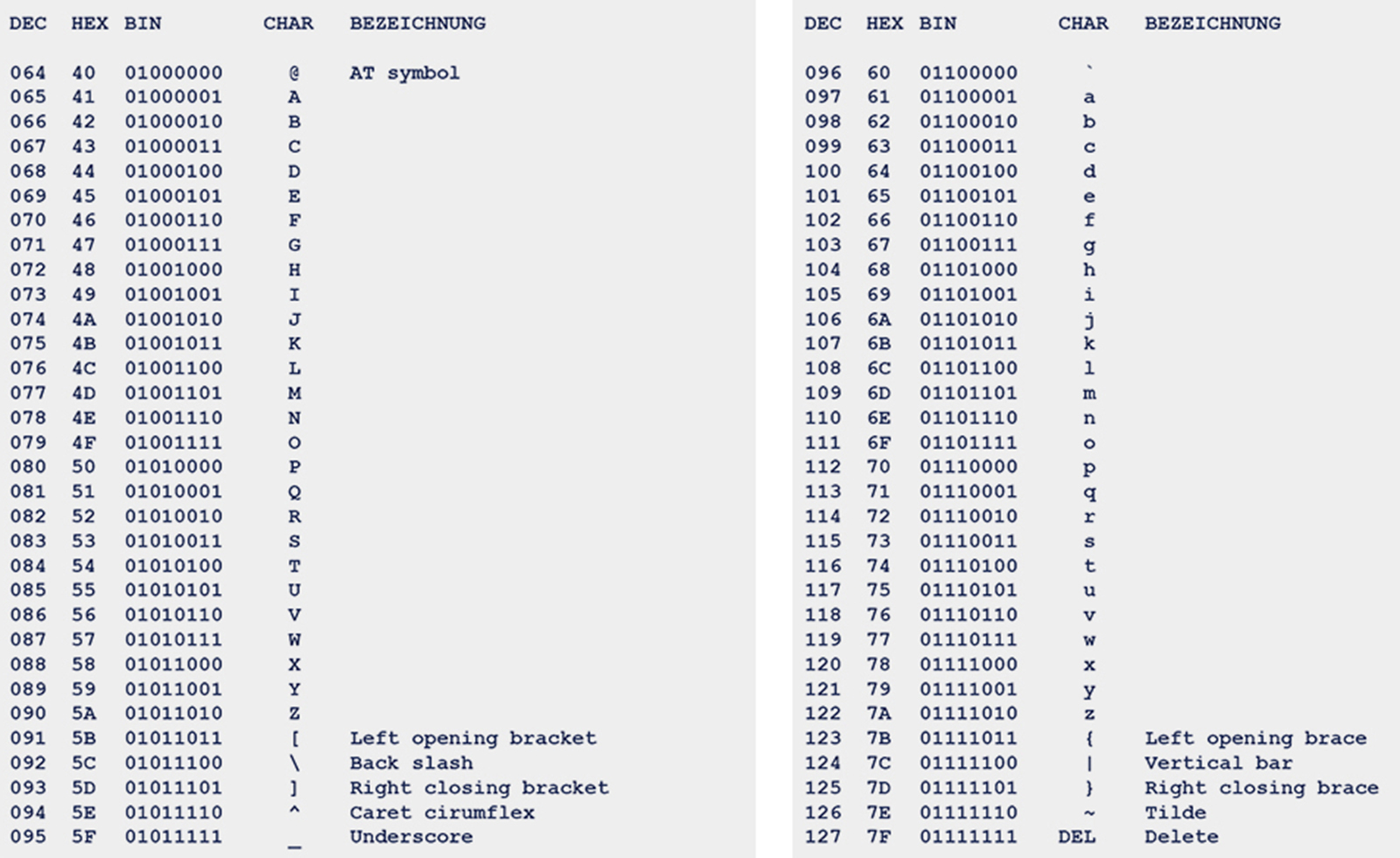Beim erweiterten ASCII-Zeichensatz kommt ein weiteres Bit dazu und der Code wird somit 8-Bit breit. Die dabei zusätzlich zur Verfügung stehenden 128 Bitkombinationen werden je nach am PC eingestellten ISO-Standard 8859 länderspezifisch anders belegt.

ASCII-Erweiterung gemäss ISO 8859

ISO: International Organization for Standardization / Internationale Organisation für Normung)
ASCII belegte bekanntlich ursprünglich 7 Bit pro Character (0...127) und wurde später um ein Bit auf 8 Bit (0...255) erweitert. Um den verschiedenen Sprachen gerecht zu werden, wurde der ISO-Standard 8859 definiert, der nun im zweiten Teil des ASCII-Zeichensatz (128...255) deren 16 Sprachzusätze unterscheidet:

• ISO-Standard 8859-1 = ANSI-ASCII (ANSI: American National Standards Institute)
• ISO-Standard 8859-1 = Latin-1, Westeuropäisch oder ANSI-ASCI
• ISO-Standard 8859-2 = Latin-2, Mitteleuropäisch
• ISO-Standard 8859-3 = Latin-3, Südeuropäisch
• ISO-Standard 8859-4 = Latin-4, Nordeuropäisch
• ISO-Standard 8859-5 = Kyrillisch
• ISO-Standard 8859-6 = Arabisch
• ISO-Standard 8859-7 = Griechisch
• ISO-Standard 8859-8 = Hebräisch
• ISO-Standard 8859-9 = Latin-5, Türkisch
• ISO-Standard 8859-10 = Latin-6, Nordisch
• ISO-Standard 8859-11 = Thai
• ISO-Standard 8859-12 = (existiert nicht)
• ISO-Standard 8859-13 = Latin-7, Baltisch
• ISO-Standard 8859-14 = Latin-8, Keltisch
• ISO-Standard 8859-15 = Latin-9, Westeuropäisch
• ISO-Standard 8859-16 = Latin-10, Südosteuropäisch

5.2 Unicode & Unicode-Codierung UTF-8 und UTF-16

Der ASCII-Code mit seinen 256 Zeichen genügt den heutigen Anforderungen nicht mehr. Es fehlen z.B. die chinesische Schriftzeichen oder wie wär's mit einem Violinschlüssel? Es muss ein umfangreicherer Zeichencode her, nämlich der Unicode.

Unicode

• Der Unicode kann max. 8 Byte lang sein (64 Bit): U+XXXX'XXXX
• Unicode V2.0 nützt bisher erst 1‘114‘112 verschiedene Zeichen U+0000'0000 bis U+0010'FFFF
• Die verbreitetste Kodierungsform ist UTF-8 und belegt pro Zeichen 1, 2, 3 oder 4 Byte
• Ebenfalls weit verbreitet ist UTF-16 und belegt pro Zeichen 2 oder 4 Byte

UTF-8

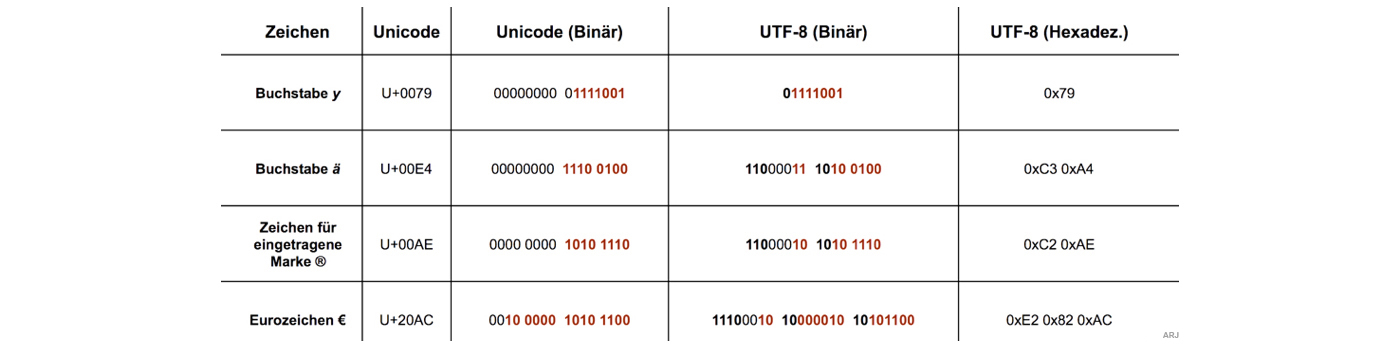
UTF-8 (UCS Transformation Format 8-Bit → UCS=Universal-Coded-Character-Set) ist die am weitesten verbreitete Kodierung für Unicode-Zeichen

• Das erste Byte eines UTF-8-kodierten Zeichens nennt man dabei Start-Byte, weitere Bytes nennt man Folgebytes. Startbytes enthalten also die Bitfolge 11xxxxxx oder 0xxxxxxx, Folgebytes immer die Bitfolge 10xxxxxx
• Ist das höchste Bit des ersten Bytes 0, handelt es sich um ein gewöhnliches ASCII-Zeichen, da ASCII eine 7-Bit-Kodierung ist und die ersten 128 Unicode-Zeichen den ASCII-Zeichen entsprechen. Damit sind alle ASCII-Dokumente automatisch aufwärtskompatibel zu UTF-8
• Ist das höchste Bit des ersten Bytes 1, handelt es sich um ein Mehrbytezeichen, also ein Unicode-Zeichen mit einer Zeichennummer grösser als 127
• Sind die höchsten beiden Bits des ersten Bytes 11, handelt es sich um das Start-Byte eines Mehrbytezeichens, sind sie 10, um ein Folge-Byte
• Die lexikalische Ordnung nach Byte-Werten entspricht der lexikalischen Ordnung nach Buchstaben-Nummern, da höhere Zeichennummern mit entsprechend mehr 1-Bits im Start-Byte kodiert werden
• Bei den Start-Bytes von Mehrbyte-Zeichen gibt die Anzahl der höchsten 1-Bits die gesamte Bytezahl des als Mehrbyte-Zeichen kodierten Unicode-Zeichens an. Anders interpretiert, die Anzahl der 1-Bits links des höchsten 0-Bits entspricht der Anzahl an Folgebytes plus eins, z. B. 1110xxxx 10xxxxxx 10xxxxxx = drei Bits vor dem höchsten 0-Bit = drei Bytes insgesamt, zwei Bits nach dem höchsten 1-Bit vor dem höchsten 0-Bit = zwei Folgebytes
• Start-Bytes (0xxx xxxx oder 11xx xxxx) und Folge-Bytes (10xx xxxx) lassen sich eindeutig voneinander unterscheiden. Somit kann ein Byte-Strom auch in der Mitte gelesen werden, ohne dass es Probleme mit der Dekodierung gibt, was insbesondere bei der Wiederherstellung defekter Daten wichtig ist. 10xxxxxx Bytes werden einfach übersprungen, bis ein 0xxxxxxx oder 11xxxxxx Byte gefunden wird. Könnten Start-Bytes und Folge-Bytes nicht eindeutig voneinander unterschieden werden, wäre das Lesen eines UTF-8-Datenstroms, dessen Beginn unbekannt ist, unter Umständen nicht möglich
• Das gleiche Zeichen kann theoretisch auf verschiedene Weise kodiert werden (Zum Beispiel „a“ als 0110 0001 oder fälschlich als 11000001 10100001). Jedoch ist nur die jeweils kürzest mögliche Kodierung erlaubt

UTF-8 Eingabemethoden

• Notation bei HTML und XML: � für dezimale Notation bzw. � für hexadezimale Notation, wobei das 0000 die Unicode-Nummer des Zeichens darstellt
• Ab Windows 2000 kann in einigen Programmen (genauer in RichEdit-Feldern) der Code dezimal als Alt+<dezimaler Unicode> auf dem numerischen Tastaturfeld eingegeben werden
• Ab Microsoft Word 2002 kann Unicode auch hexadezimal eingegeben werden, indem im Dokument <Unicode> oder U+<Unicode> eingetippt wird und anschließend die Tastenkombination Alt+C im Dokument bzw. Alt+X in Dialog-feldern gedrückt wird
• In Powerpoint: Alt-Taste gedrückt halten und auf dem Zahlenblock den Unicode in Dezimal eingeben. Z.B. Für den Pipe: Unicode in Hexadezimal 007c in Dezimal 124. Somit ALT + 124 (Auf dem Zahlenblock eingeben)
• Ob das entsprechende Unicode-Zeichen auch tatsächlich am Bildschirm erscheint, hängt davon ab, ob die verwendete Schriftart/Fonttype eine Glyphe für das gewünschte Zeichen (also eine Grafik für die gewünschte Zeichen-Nummer) enthält. WIN: Siehe charmap.exe

UTF-16

Ein UTF-16-Character besteht je nach Unicode-Zeichen aus 16 Bit oder 32 Bit.

• 16 Bit UTF16-Zeichen: Für Unicodezeichen U+0000 bis U+D7FF und U+E000 bis U+FFFF.
• 32 Bit UTF16-Zeichen: Für Unicodezeichen U+10000 bis U+10FFFF.

Byte-Order LE und BE

Die Bytereihenfolge (Byteorder, Endianness) bezeichnet in der Computertechnik die Speicherorganisation für einfache Zahlenwerte, bzw. die Ablage ganzzahliger Werte (Integer) im Arbeitsspeicher. Auch beim UTF16 muss man sich für die eine oder andere Byteorder entscheiden.

• BE: Big-Endian. Das höchstwertigste Byte wird zuerst, bzw. an der kleinsten Speicheradresse gespeichert. Die grösstwertigste Komponente wird zuerst genannt, wie z.B. bei der Uhrzeit: Stunde.Minute.
• LE: Little-Endian. Das kleinstwertigste Byte wird an der Anfangsadresse gespeichert, also die kleinstwertige Komponente zuerst genannt, wie z.B. beim Datum: Monat.Jahr.

• UTF16-BE-BOM: FE FF
• UTF16-LE-BOM: FF FE